
【题目】设函数f(x)=xex﹣asinxcosx(a∈R,其中e是自然对数的底数).
(1)当a=0时,求f(x)的极值;
(2)若对于任意的x∈[0, ![]() ],f(x)≥0恒成立,求a的取值范围;
],f(x)≥0恒成立,求a的取值范围;
(3)是否存在实数a,使得函数f(x)在区间 ![]() 上有两个零点?若存在,求出a的取值范围;若不存在,请说明理由.
上有两个零点?若存在,求出a的取值范围;若不存在,请说明理由.
【答案】
(1)解:当a=0时,f(x)=xex,f′(x)=ex(x+1),
令f′(x)=0,得x=﹣1,
列表如下:
x | (﹣∞,﹣1) | ﹣1 | (﹣1,+∞) |
f′(x) | + | 0 | ﹣ |
f(x) | ↘ | 极小值 | ↗ |
所以函数f(x)的极小值为 ![]() ,无极大值
,无极大值
(2)解:①当a≤0时,由于对于任意 ![]() ,有sinxcosx≥0,
,有sinxcosx≥0,
所以f(x)≥0恒成立,当a≤0时,符合题意;
②当0<a≤1时,因为f′(x)≥ex(x+1)﹣acos2x≥e0(0+1)﹣acos0=1﹣a≥0,
所以函数f(x)在 ![]() 上为增函数,所以f(x)≥f(0)=0,即当0<a≤1,符合题意;
上为增函数,所以f(x)≥f(0)=0,即当0<a≤1,符合题意;
③当a>1时,f′(0)=1﹣a<0, ![]() ,
,
所以存在 ![]() ,使得f′(α)=0,且在(0,α)内,f′(x)<0,
,使得f′(α)=0,且在(0,α)内,f′(x)<0,
所以f(x)在(0,α)上为减函数,所以f(x)<f(0)=0,
即当a>1时,不符合题意,
综上所述,a的取值范围是(﹣∞,1]
(3)解:不存在实数a,使得函数f(x)在区间 ![]() 上有两个零点,
上有两个零点,
由(2)知,当a≤1时,f(x)在 ![]() 上是增函数,且f(0)=0,
上是增函数,且f(0)=0,
故函数f(x)在区间 ![]() 上无零点,
上无零点,
当a>1时,f′(x)≥ex(x+1)﹣acos2x,
令g(x)=ex(x+1)﹣acos2x,g′(x)=ex(x+2)+2asin2x
当 ![]() 时,恒有g′(x)>0,所以g(x)在
时,恒有g′(x)>0,所以g(x)在 ![]() 上是增函数,
上是增函数,
由 ![]() ,
,
故g(x)在 ![]() 上存在唯一的零点x0,即方程f′(x)=0在
上存在唯一的零点x0,即方程f′(x)=0在 ![]() 上存在唯一解x0,
上存在唯一解x0,
且当x∈(0,x0)时,f′(x)<0,当 ![]() ,f′(x)>0,
,f′(x)>0,
即函数f(x)在(0,x0)上单调递减,在 ![]() 上单调递增,
上单调递增,
当x∈(0,x0)时,f(x)<f(0)=0,即f(x)在(0,x0)无零点;
当 ![]() 时,
时, ![]() ,
,
所以f(x)在 ![]() 上有唯一零点,
上有唯一零点,
所以,当a>1时,f(x)在 ![]() 上有一个零点,
上有一个零点,
综上所述,不存在实数a,使得函数f(x)在区间 ![]() 上有两个零点
上有两个零点
【解析】(1)将a=0代入f(x),求出函数的导数,列出表格,求出函数的极值即可;(2)通过讨论a的范围,求出函数的导数,确定函数的单调区间,从而确定a的范围即可;(3)求出当a≤1时,函数f(x)在区间 ![]() 上无零点,a>1时,求出函数的导数,根据函数的单调性得到f(x)在
上无零点,a>1时,求出函数的导数,根据函数的单调性得到f(x)在 ![]() 上有一个零点,从而判断结论即可.
上有一个零点,从而判断结论即可.
【考点精析】解答此题的关键在于理解函数的极值与导数的相关知识,掌握求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值,以及对函数的最大(小)值与导数的理解,了解求函数
是极小值,以及对函数的最大(小)值与导数的理解,了解求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值.
比较,其中最大的是一个最大值,最小的是最小值.


科目:高中数学 来源: 题型:
【题目】给出两个命题:
命题甲:关于x的不等式x2+(a﹣1)x+a2≤0的解集为;
命题乙:函数y=(2a2﹣a)x为增函数.
(1)甲、乙至少有一个是真命题;
(2)甲、乙有且只有一个是真命题;
分别求出符合(1)(2)的实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,椭圆C: ![]() =1(a>1)的左、右顶点分别为A、B,P是椭圆C上任一点,且点P位于第一象限.直线PA交y轴于点Q,直线PB交y轴于点R.当点Q坐标为(0,1)时,点R坐标为(0,2)
=1(a>1)的左、右顶点分别为A、B,P是椭圆C上任一点,且点P位于第一象限.直线PA交y轴于点Q,直线PB交y轴于点R.当点Q坐标为(0,1)时,点R坐标为(0,2) 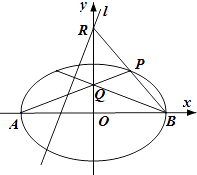
(1)求椭圆C的标准方程;
(2)求证: ![]() 为定值;
为定值;
(3)求证:过点R且与直线QB垂直的直线经过定点,并求出该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动圆过定点P(4,0),且在y轴上截得的弦MN的长为8.
(1)求动圆圆心C的轨迹方程;
(2)过点(2,0)的直线l与动圆圆心C的轨迹交于A,B两点,求证:![]() 是一个定值.
是一个定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() (a>b>0)的离心率为
(a>b>0)的离心率为![]() ,以坐标原点O为圆心,椭圆C的短半轴长为半径的圆与直线x+y+
,以坐标原点O为圆心,椭圆C的短半轴长为半径的圆与直线x+y+![]() =0相切.A,B分别是椭圆C的左、右顶点,直线l过B点且与x轴垂直.
=0相切.A,B分别是椭圆C的左、右顶点,直线l过B点且与x轴垂直.
(1)求椭圆C的标准方程;
(2)设G是椭圆C上异于A,B的任意一点,过点G作GH⊥x轴于点H,延长HG到点Q使得|HG|=|GQ|,连接AQ并延长交直线l于点M,N为线段MB的中点,判断直线QN与以AB为直径的圆O的位置关系,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲,乙两人进行围棋比赛,共比赛2n(n∈N+)局,根据以往比赛胜负的情况知道,每局甲胜的概率和乙胜的概率均为 ![]() .如果某人获胜的局数多于另一人,则此人赢得比赛.记甲赢得比赛的概率为P(n).
.如果某人获胜的局数多于另一人,则此人赢得比赛.记甲赢得比赛的概率为P(n).
(1)求P(2)与P(3)的值;
(2)试比较P(n)与P(n+1)的大小,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知椭圆 ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,长轴长为4,过椭圆的左顶点A作直线l,分别交椭圆和圆x2+y2=a2于相异两点P,Q.
,长轴长为4,过椭圆的左顶点A作直线l,分别交椭圆和圆x2+y2=a2于相异两点P,Q. 
(1)若直线l的斜率为 ![]() ,求
,求 ![]() 的值;
的值;
(2)若 ![]() =λ
=λ ![]() ,求实数λ的取值范围.
,求实数λ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲,乙两人进行围棋比赛,共比赛2n(n∈N+)局,根据以往比赛胜负的情况知道,每局甲胜的概率和乙胜的概率均为 ![]() .如果某人获胜的局数多于另一人,则此人赢得比赛.记甲赢得比赛的概率为P(n).
.如果某人获胜的局数多于另一人,则此人赢得比赛.记甲赢得比赛的概率为P(n).
(1)求P(2)与P(3)的值;
(2)试比较P(n)与P(n+1)的大小,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com