
【题目】唐三彩,中国古代陶瓷烧制工艺的珍品,它吸取了中国国画、雕塑等工艺美术的特点,在中国文化中占有重要的历史地位,在中国的陶瓷史上留下了浓墨重彩的一笔,唐三彩的生产至今已有1300多年的历史,对唐三彩的复制和仿制工艺,至今也有百余年的历史.某陶瓷厂在生产过程中,对仿制的100件工艺品测得其重量(单位;kg)数据,将数据分组如下表:

(1)在答题卡上完成频率分布表;
(2)重量落在![]() 中的频率及重量小于2.45的频率是多少?
中的频率及重量小于2.45的频率是多少?
(3)统计方法中,同一组数据常用该组区间的中点值(例如区间![]() 的中点值是
的中点值是![]() 作为代表.据此,估计这100个数据的平均值.
作为代表.据此,估计这100个数据的平均值.
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:高中数学 来源: 题型:
【题目】集合![]() 由满足以下性质的函数
由满足以下性质的函数![]() 组成:①
组成:①![]() 在
在![]() 上是增函数;②对于任意的
上是增函数;②对于任意的![]() ,
, ![]() .已知函数
.已知函数![]() ,
, ![]() .
.
(1)试判断![]() ,
, ![]() 是否属于集合
是否属于集合![]() ,并说明理由;
,并说明理由;
(2)将(1)中你认为属于集合![]() 的函数记为
的函数记为![]() .
.
(ⅰ)试用列举法表示集合![]() ;
;
(ⅱ)若函数![]() 在区间
在区间![]() 上的值域为
上的值域为![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了绿化城市,要在矩形区域ABCD内建一个矩形草坪,如图所示,另外,△AEF内部有一文物保护区不能占用,经测量AB=100 m,BC=80 m,AE=30 m,AF=20 m,应如何设计才能使草坪面积最大?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某县政府为了引导居民合理用水,决定全面实施阶梯水价,阶梯水价原则上以住宅(一套住宅为一户)的月用水量为基准定价:若用水量不超过12吨时,按4元/吨计算水费;若用水量超过12吨且不超过14吨时,超过12吨部分按6.60元/吨计算水费;若用水量超过14吨时,超过14吨部分按7.80元/吨计算水费.为了了解全市居民月用水量的分布情况,通过抽样,获得了100户居民的月用水量(单位:吨),将数据按照![]() ,
,![]() ,…,
,…,![]() 分成8组,制成了如图1所示的频率分布直方图.
分成8组,制成了如图1所示的频率分布直方图.
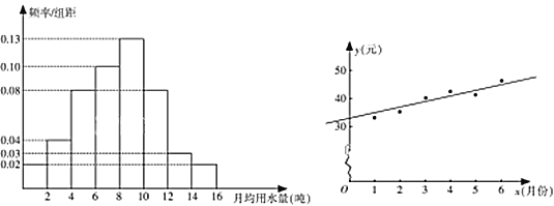
(图1) (图2)
(Ⅰ)通过频率分布直方图,估计该市居民每月的用水量的平均数和中位数(精确到0.01);
(Ⅱ)求用户用水费用![]() (元)关于月用水量
(元)关于月用水量![]() (吨)的函数关系式;
(吨)的函数关系式;
(Ⅲ)如图2是该县居民李某2017年1~6月份的月用水费![]() (元)与月份
(元)与月份![]() 的散点图,其拟合的线性回归方程是
的散点图,其拟合的线性回归方程是![]() .若李某2017年1~7月份水费总支出为294.6元,试估计李某7月份的用水吨数.
.若李某2017年1~7月份水费总支出为294.6元,试估计李某7月份的用水吨数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】浦东新区某镇投入资金进行生态环境建设,2017年度计划投入800万元,以后每年投入将比上一年减少 ![]() ,今年该镇旅游收入估计500万元,由于该项建设对旅游的促进作用,预计今后的旅游收入每年会比上一年增加
,今年该镇旅游收入估计500万元,由于该项建设对旅游的促进作用,预计今后的旅游收入每年会比上一年增加 ![]() ;
;
(1)设n年内(今年为第一年)总投入为an万元,旅游总收入为bn万元,写出an , bn的表达式;
(2)至少经过几年,旅游业的总收入才能超过总投入.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】相传古代印度国王在奖赏他聪明能干的宰相达依尔(国际象棋发明者)时,问他需要什么,达依尔说:“国王只要在国际象棋棋盘的第一格子上放一粒麦子,第二格子上放二粒,第三格子上放四粒,以后按比例每一格加一倍,一直放到第64格(国际象棋棋盘格数是8×8=64),我就感恩不尽,其他什么也不要了.”国王想:“这才有多少,还不容易!”于是让人扛来一袋小麦,但不到一会儿就用完了,再来一袋很快又没有了,结果全印度的粮食用完还不够,国王很奇怪,怎么也算不清这笔账.请你设计一个程序框图表示其算法,来帮国王计算一下需要多少粒小麦.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:方程x2+mx+1=0有两个不相等的实根;
命题q:函数f(x)=lg[x2﹣2(m+1)x+m(m+1)]的定义域为R,
若“p∨q”为真,“p∧q”为假,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=xlnx.
(1)求f(x)的单调区间和极值;
(2)设A(x1 , f(x1)),B(x2 , f(x2)),且x1≠x2 , 证明: ![]() <f′(
<f′( ![]() ).
).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com