
【题目】已知椭圆![]() 的方程为
的方程为![]() ,圆
,圆![]() 与
与![]() 轴相切于点
轴相切于点![]() ,与
,与![]() 轴正半轴相交于
轴正半轴相交于![]() 、
、![]() 两点,且
两点,且![]() ,如图1.
,如图1.
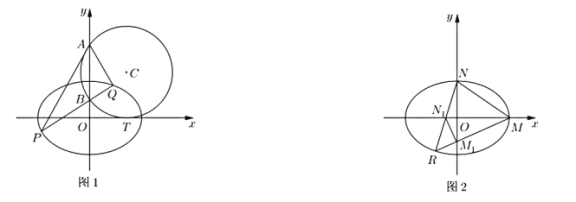
(1)求圆![]() 的方程;
的方程;
(2)如图1,过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 、
、![]() 两点,求证:射线
两点,求证:射线![]() 平分
平分![]() ;
;
(3)如图2所示,点![]() 、
、![]() 是椭圆
是椭圆![]() 的两个顶点,且第三象限的动点
的两个顶点,且第三象限的动点![]() 在椭圆
在椭圆![]() 上,若直线
上,若直线![]() 与
与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,试问:四边形
,试问:四边形![]() 的面积是否为定值?若是,请求出这个定值,若不是,请说明理由.
的面积是否为定值?若是,请求出这个定值,若不是,请说明理由.
科目:高中数学 来源: 题型:
【题目】某高速公路隧道设计为单向三车道,每条车道宽4米,要求通行车辆限高5米,隧道全长1.5千米,隧道的断面轮廓线近似地看成半个椭圆形状(如图所示).

(1)若最大拱高![]() 为6米,则隧道设计的拱宽
为6米,则隧道设计的拱宽![]() 至少是多少米?(结果取整数)
至少是多少米?(结果取整数)
(2)如何设计拱高![]() 和拱宽
和拱宽![]() ,才能使半个椭圆形隧道的土方工程量最小?(结果取整数)
,才能使半个椭圆形隧道的土方工程量最小?(结果取整数)
参考数据:![]() ,椭圆的面积公式为
,椭圆的面积公式为![]() ,其中
,其中![]() ,
,![]() 分别为椭圆的长半轴和短半轴长.
分别为椭圆的长半轴和短半轴长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4—5:参数方程选讲]
在直角坐标系xoy中,曲线![]() 的参数方程是
的参数方程是 (t是参数),以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线
(t是参数),以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程是
的极坐标方程是![]()
(1)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若两曲线交点为A、B,求![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某机器生产商,对一次性购买两台机器的客户推出两种超过质保期后两年内的延保维修方案:
方案一:交纳延保金![]() 元,在延保的两年内可免费维修
元,在延保的两年内可免费维修![]() 次,超过
次,超过![]() 次每次收取维修费
次每次收取维修费![]() 元;
元;
方案二:交纳延保金![]() 元,在延保的两年内可免费维修
元,在延保的两年内可免费维修![]() 次,超过
次,超过![]() 次每次收取维修费
次每次收取维修费![]() 元.
元.
某工厂准备一次性购买两台这种机器,现需决策在购买机器时应购买哪种延保方案,为此搜集并整理了台这种机器超过质保期后延保两年内维修的次数,统计得下表:
维修次数 | 0 | 1 | 2 | 3 |
机器台数 | 20 | 10 | 40 | 30 |
以上![]() 台机器维修次数的频率代替一台机器维修次数发生的概率,记
台机器维修次数的频率代替一台机器维修次数发生的概率,记![]() 表示这两台机器超过质保期后延保两年内共需维修的次数.
表示这两台机器超过质保期后延保两年内共需维修的次数.
![]() 求
求![]() 的分布列;
的分布列;
![]() 以所需延保金与维修费用之和的期望值为决策依据,该工厂选择哪种延保方案更合算?
以所需延保金与维修费用之和的期望值为决策依据,该工厂选择哪种延保方案更合算?
查看答案和解析>>
科目:高中数学 来源: 题型:
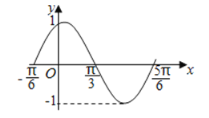
【题目】如图是函数![]() (
(![]() ,
,![]() ,
,![]() ,
,![]() )在区间
)在区间![]() 上的图象,为了得到这个函数的图象,只需将
上的图象,为了得到这个函数的图象,只需将![]() (
(![]() )的图象上的所有的点( )
)的图象上的所有的点( )
A. 向左平移![]() 个长度单位,再把所得各点的横坐标变为原来的
个长度单位,再把所得各点的横坐标变为原来的![]() ,纵坐标不变
,纵坐标不变
B. 向左平移![]() 个长度单位,再把所得各点的横坐标变为原来的2倍,纵坐标不变
个长度单位,再把所得各点的横坐标变为原来的2倍,纵坐标不变
C. 向左平移![]() 个长度单位,再把所得各点的横坐标变为原来的
个长度单位,再把所得各点的横坐标变为原来的![]() ,纵坐标不变
,纵坐标不变
D. 向左平移![]() 个长度单位,再把所得各点的横坐标变为原来的2倍,纵坐标不变
个长度单位,再把所得各点的横坐标变为原来的2倍,纵坐标不变
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的焦距为
的焦距为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,且
上,且![]() 的最小值是
的最小值是![]() (
(![]() 为坐标原点).
为坐标原点).
(1)求椭圆![]() 的标准方程.
的标准方程.
(2)已知动直线![]() 与圆
与圆![]() :
:![]() 相切,且与椭圆
相切,且与椭圆![]() 交于
交于![]() ,
,![]() 两点.是否存在实数
两点.是否存在实数![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com