
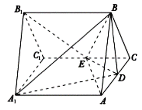
【题目】如图,三棱柱![]() 的所有棱长都是2,
的所有棱长都是2,![]() 平面ABC,D,E分别是AC,
平面ABC,D,E分别是AC,![]() 的中点.
的中点.
(1)求证:![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见证明;(2)![]()
【解析】
(1)利用线面垂直的判定和性质,得到![]() 平面
平面![]() ,进而证得
,进而证得![]() ;
;
(2)建立空间直角坐标系,求面DBE和面![]() 的法向量,利用向量的夹角公式,即可求得二面角
的法向量,利用向量的夹角公式,即可求得二面角![]() 的余弦值.
的余弦值.
(1)∵![]() ,D是AC的中点,∴
,D是AC的中点,∴![]() ,
,
∵![]() 平面ABC,∴平面
平面ABC,∴平面![]() 平面ABC,
平面ABC,
∴![]() 平面
平面![]() ,∴
,∴![]() .
.
又∵在正方形![]() 中,D,E分别是AC,
中,D,E分别是AC,![]() 的中点,易证得∴△A1AD≌△ACE
的中点,易证得∴△A1AD≌△ACE
∴∠A1DA=∠AEC, ∵∠AEC+∠CAE=90°,∴∠A1DA+∠CAE=90° ,即![]() .
.
又![]() ,∴
,∴![]() 平面
平面![]() .
.
又![]() ,则
,则![]()
(2)取![]() 中点F,以DF,DA,DB为x,y,z轴建立空间直角坐标系
中点F,以DF,DA,DB为x,y,z轴建立空间直角坐标系

![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
设平面DBE的一个法向量为![]() ,
,
则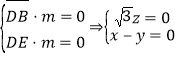 ,
,
令![]() ,则
,则![]() ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则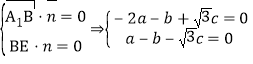 ,
,
令![]() ,则
,则![]() ,
,
设二面角![]() 的平面角为
的平面角为![]() ,观察可知
,观察可知![]() 为锐角,
为锐角,
![]()
故二面角![]() 的余弦值为
的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】在某公司举行的年终庆典活动中,主持人利用随机抽奖软件进行抽奖:由电脑随机生成一张如图所示的3![]() 3表格,其中1格设奖300元,4格各设奖200元,其余4格各设奖100元,点击某一格即显示相应金额.某人在一张表中随机不重复地点击3格,记中奖的总金额为X元.
3表格,其中1格设奖300元,4格各设奖200元,其余4格各设奖100元,点击某一格即显示相应金额.某人在一张表中随机不重复地点击3格,记中奖的总金额为X元.
(1)求概率![]() ;
;
(2)求![]() 的概率分布及数学期望
的概率分布及数学期望![]() .
.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我们学校是一所有着悠久传统文化的学校,我们学校全名叫重庆外国语学校(Chongqing Foreign Language School),又名四川外国语大学附属外国语学校,简称“重外”,1981年,被定为四川省首批办好的重点中学;1997年,被列为重庆市教委首批办好的直属重点中学之一;2001年被国家教育部指定为20%高三学生享有保送资格的全国十三所学校之一,今年我校保送取得了非常辉煌的成绩,目前为止,包括清华大学,北京大学在内目前共保送122名同学,其中北京大学,南开大学,北京外国语大学保送的人数成公差为正数的等差数列,三个学校保送人数之和为24人,三个学校保送学生人数之积为312,则北京外国语大学保送的人数为(以上数据均来自于学校官网)( )
A.10B.11C.13D.14
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知曲线![]() 的极坐标方程是
的极坐标方程是![]() ,以极点为平面直角坐标系的原点,极轴为
,以极点为平面直角坐标系的原点,极轴为![]() 轴的正半轴,建立平面直角坐标系,直线
轴的正半轴,建立平面直角坐标系,直线![]() 的参数方程是
的参数方程是![]() (
(![]() 是参数),
是参数),
(Ⅰ)写出直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设曲线![]() 经过伸缩变换
经过伸缩变换![]() 得到曲线
得到曲线![]() ,曲线
,曲线![]() 任一点为
任一点为![]() ,求点
,求点![]() 直线
直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图![]() ,
,![]() 是以
是以![]() 为直径的圆上一段圆弧,
为直径的圆上一段圆弧,![]() 是以
是以![]() 为直径的圆上一段圆弧,
为直径的圆上一段圆弧,![]() 是以
是以![]() 为直径的圆上一段圆弧,三段弧构成曲线
为直径的圆上一段圆弧,三段弧构成曲线![]() .则下面说法正确的是( )
.则下面说法正确的是( )

A.曲线![]() 与
与![]() 轴围成的面积等于
轴围成的面积等于![]()
B.![]() 与
与![]() 的公切线方程为:
的公切线方程为:![]()
C.![]() 所在圆与
所在圆与![]() 所在圆的交点弦方程为:
所在圆的交点弦方程为:![]()
D.用直线![]() 截
截![]() 所在的圆,所得的弦长为
所在的圆,所得的弦长为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知直线![]() 与圆O:
与圆O:![]() 相切.
相切.
(1)直线l过点(2,1)且截圆O所得的弦长为![]() ,求直线l的方程;
,求直线l的方程;
(2)已知直线y=3与圆O交于A,B两点,P是圆上异于A,B的任意一点,且直线AP,BP与y轴相交于M,N点.判断点M、N的纵坐标之积是否为定值?若是,求出该定值;若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高一举行了一次数学竞赛,为了了解本次竞赛学生的成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为![]() )作为样本(样本容量
)作为样本(样本容量![]() )进行统计,按照
)进行统计,按照![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 的分组作出频率分布直方图,已知得分在
的分组作出频率分布直方图,已知得分在![]() 、
、![]() 的频数分别为
的频数分别为![]() 、
、![]() .
.
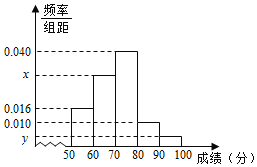
(1)求样本容量![]() 和频率分布直方图中的
和频率分布直方图中的![]() 、
、![]() 的值;
的值;
(2)估计本次竞赛学生成绩的众数、中位数、平均数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com