
【题目】如图,在矩形ABCD中, ![]() ,点E,H分别是所在边靠近B,D的三等分点,现沿着EH将矩形折成直二面角,分别连接AD,AC,CB,形成如图所示的多面体.
,点E,H分别是所在边靠近B,D的三等分点,现沿着EH将矩形折成直二面角,分别连接AD,AC,CB,形成如图所示的多面体.

(1)证明:平面BCE∥平面ADH;
(2)证明:EH⊥AC;
(3)求二面角B-AC-D的平面角的余弦值.
【答案】(1)见解析(2)![]() .
.
【解析】试题分析:(1)根据折叠前、后不变量得AH∥BE,DH∥EC,根据线面平行判定定理得AH∥平面BCE,DH∥平面BCE,再根据面面平行判定定理得平面BCE∥平面ADH.(2)先过点A作EH的垂线交EH于点O,由面面垂直性质定理得AO⊥平面EHC,再由直二面角定义得CO⊥EH,因此根据线面垂直判定定理得EH⊥平面AOC,即得EH⊥AC.(3)根据条件作出二面角B-AC-O平面角![]() BQP,并根据直角三角形求出
BQP,并根据直角三角形求出![]() ,最后根据二面角B-AC-D的平面角为
,最后根据二面角B-AC-D的平面角为![]() BQP,并利用二倍角余弦公式求值.
BQP,并利用二倍角余弦公式求值.
试题解析:(1)证明:由折叠前、后图形对比可知,在矩形ABCD中有AH∥BE,DH∥EC,
又∵AH∩DH=H,BE∩CE=E,∴平面BCE∥平面ADH.
(2)证明:在多面体中,过点A作EH的垂线交EH于点O,连接OC.
∵二面角A-EH-C为直二面角,∴AO⊥平面EHC.
由对称性可知CO⊥EH,又AO∩CO=O.
∴EH⊥平面AOC,而![]() 平面AOC,∴EH⊥AC.
平面AOC,∴EH⊥AC.
(3)解:过点B在平面ABEH内作BP⊥AO垂足为P,过点P在平面AOC内作PQ⊥AC垂足为Q,连接BQ.∵△ABO是边长为3的等边三角形,∴点P为中点, ![]() .
.
∵△AOC是直角边长为3的等腰直角三角形![]() ,∴
,∴![]() .
.
又∵CO⊥平面ABEH,∴CO⊥BP,BP⊥AO,AO∩CO=O,∴BP⊥平面AOC.
∴![]() BQP为二面角B-AC-O的平面角,在直角三角形BPQ中
BQP为二面角B-AC-O的平面角,在直角三角形BPQ中![]() ,
,
∴![]() .
.
设二面角B-AC-D的平面角为![]() ,∴
,∴![]() .
.
所以二面角B-AC-D的平面角的余弦值为![]() .
.


 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(sinx,cosx),
=(sinx,cosx), ![]() =(sin(x﹣
=(sin(x﹣ ![]() ),sinx),函数f(x)=2
),sinx),函数f(x)=2 ![]()
![]() ,g(x)=f(
,g(x)=f( ![]() ).
).
(1)求f(x)在[ ![]() ,π]上的最值,并求出相应的x的值;
,π]上的最值,并求出相应的x的值;
(2)计算g(1)+g(2)+g(3)+…+g(2014)的值;
(3)已知t∈R,讨论g(x)在[t,t+2]上零点的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数f(x)=sin2x的图象向右平移φ(0<φ< ![]() )个单位后得到函数g(x)的图象.若对满足|f(x1)﹣g(x2)|=2的x1、x2 , 有|x1﹣x2|min=
)个单位后得到函数g(x)的图象.若对满足|f(x1)﹣g(x2)|=2的x1、x2 , 有|x1﹣x2|min= ![]() ,则φ=( )
,则φ=( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+φ),x∈R(其中 ![]() )的图象与x轴的交点中,相邻两个交点之间的距离为
)的图象与x轴的交点中,相邻两个交点之间的距离为 ![]() ,且图象上一个最低点为
,且图象上一个最低点为 ![]() .
.
(1)求f(x)的解析式;
(2)当 ![]() ,求f(x)的值域.
,求f(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知椭圆![]() 的半焦距为c,且过点
的半焦距为c,且过点![]() ,原点O到经过两点(c,0),(0,b)的直线的距离为
,原点O到经过两点(c,0),(0,b)的直线的距离为![]() .
.

(1)求椭圆E的方程;
(2)A为椭圆E上异于顶点的一点,点P满足![]() ,过点P的直线交椭圆E于B,C两点,且
,过点P的直线交椭圆E于B,C两点,且![]() ,若直线OA,OB的斜率之积为
,若直线OA,OB的斜率之积为![]() ,求证:
,求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三棱锥S﹣ABC中,SA⊥AB,SA⊥AC,AC⊥BC且AC=2,BC=![]() , SB=
, SB=![]() .
.
(1)证明:SC⊥BC;
(2)求三棱锥的体积VS﹣ABC
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,抛物线y=x2+bx+c与x轴交于点A和点B(3,0),与y轴交于点C(0,3).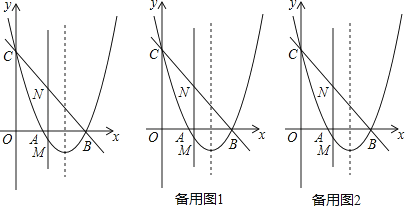
(1)求抛物线的解析式;
(2)若点M是抛物线在x轴下方上的动点,过点M作MN∥y轴交直线BC于点N,求线段MN的最大值;
(3)在(2)的条件下,当MN取得最大值时,在抛物线的对称轴l上是否存在点P,使△PBN是等腰三角形?若存在,请直接写出所有点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】百子回归图是由1,2,3…,100无重复排列而成的正方形数表,它是一部数化的澳门简史,如:中央四位“19 99 12 20”标示澳门回归日期,最后一行中间两位“23 50”标示澳门面积,…,同时它也是十阶幻方,其每行10个数之和,每列10个数之和,每条对角线10个数之和均相等,则这个和为.
. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com