
分析 (Ⅰ)由x=ρcosθ,y=ρsinθ,x2+y2=ρ2,代入半圆的极坐标方程,再由同角的平方关系,可得参数方程;
(Ⅱ)设直线l的倾斜角为α,可得直线l的方程为y=xtanα-2,D(cos2α,1+sin2α),2α∈(0,π).求得|AB|,运用点到直线的距离公式可得D到AB的距离,再由三角形的面积公式,由三角函数的恒等变换,即可得到所求点的坐标.
解答 解:(Ⅰ)由x=ρcosθ,y=ρsinθ,x2+y2=ρ2,
可得半圆C的直角坐标方程为x2+y2=2y,
即x2+(y-1)2=1(y>1),
它的参数方程是$\left\{\begin{array}{l}x=cosφ\\ y=1+sinφ\end{array}$,φ为参数且φ∈(0,π);
(Ⅱ)设直线l的倾斜角为α,
则直线l的方程为y=xtanα-2,
D(cos2α,1+sin2α),2α∈(0,π).
|AB|=$\sqrt{4+\frac{4}{ta{n}^{2}α}}$=$\frac{2}{sinα}$,
点D到直线l的距离为d=$\frac{|cos2αtanα-2-1-sin2α|}{\sqrt{1+ta{n}^{2}α}}$
=$\frac{|cos2αsinα-3cosα-sin2αcosα|}{\sqrt{co{s}^{2}α+si{n}^{2}α}}$=|-3cosα-sinα|=3cosα+sinα,
由△ABD的面积为4,得4=$\frac{1}{2}$d|AB|=$\frac{3cosα+sinα}{sinα}$=1+3cotα,
可得tanα=1,得α=$\frac{π}{4}$,
故点D为(0,2).
点评 本题考查极坐标方程和参数方程的互化,考查圆的参数方程的运用,直线方程的运用,点到直线的距离公式,同时考查三角函数的恒等变换的运用,属于中档题.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:高中数学 来源:2016-2017学年内蒙古高二理上月考一数学理试卷(解析版) 题型:解答题
已知椭圆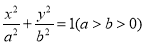 的左、右两个焦点
的左、右两个焦点 ,过其中两个端点的直线斜率为
,过其中两个端点的直线斜率为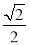 ,过两个焦点和一个顶点的三角形面积为1。
,过两个焦点和一个顶点的三角形面积为1。
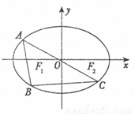
(1)求椭圆的方程;
(2)如图,点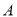 为椭圆上一动点(非长轴端点),
为椭圆上一动点(非长轴端点),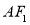 的延长线与椭圆交于
的延长线与椭圆交于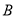 点,
点,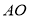 的延长线与椭圆交
的延长线与椭圆交
于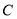 点,求
点,求 面积的最大值,并求此时直线
面积的最大值,并求此时直线 的方程,
的方程,
查看答案和解析>>
科目:高中数学 来源:2016-2017学年江西吉安一中高二上段考一数学(文)试卷(解析版) 题型:选择题
下列四个命题中错误的个数是( )
①垂直于同一条直线的两条直线相互平行;
②垂直于同一个平面的两条直线相互平行;
③垂直于同一条直线的两个平面相互平行;
④垂直于同一个平面的两个平面相互平行.
A.1 B.2 C.3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
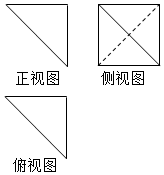 某四面体的三视图如图所示,正视图、俯视图都是腰长为2的等腰直角三角形,侧视图是边长为2的正方形,则此四面体的外接球的体积是( )
某四面体的三视图如图所示,正视图、俯视图都是腰长为2的等腰直角三角形,侧视图是边长为2的正方形,则此四面体的外接球的体积是( )| A. | 12π | B. | 48π | C. | 4$\sqrt{3}$π | D. | 32$\sqrt{3}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
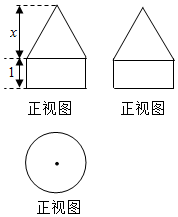 如图,是一个几何体的三视图,其中正视图与侧视图完全相同,均为等边三角形与矩形的组合,俯视图为圆,若已知该几何体的表面积为16π,则x=$2\sqrt{3}$.
如图,是一个几何体的三视图,其中正视图与侧视图完全相同,均为等边三角形与矩形的组合,俯视图为圆,若已知该几何体的表面积为16π,则x=$2\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 设Rt△ABC中,∠A=90°,AB=1,AC=$\sqrt{3}$,D是线段AC(除端点A、C)上一点,将△ABD沿BD翻折至平面A′BD,使平面A′BD⊥平面ABC,当A′在平面ABC的射影H到平面ABA′的距离最大时,AD的长度为( )
设Rt△ABC中,∠A=90°,AB=1,AC=$\sqrt{3}$,D是线段AC(除端点A、C)上一点,将△ABD沿BD翻折至平面A′BD,使平面A′BD⊥平面ABC,当A′在平面ABC的射影H到平面ABA′的距离最大时,AD的长度为( )| A. | $\root{4}{2}$ | B. | $\root{3}{2}$ | C. | $\root{4}{3}$ | D. | $\root{3}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在四棱柱ABCD-A1B1C1D1中,底面ABCD是菱形,且AB=AA1,∠A1AB=∠A1AD=60°
在四棱柱ABCD-A1B1C1D1中,底面ABCD是菱形,且AB=AA1,∠A1AB=∠A1AD=60°查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com