
【题目】已知函数f(x)= ![]() ,直线y=
,直线y= ![]() x为曲线y=f(x)的切线(e为自然对数的底数).
x为曲线y=f(x)的切线(e为自然对数的底数).
(1)求实数a的值;
(2)用min{m,n}表示m,n中的最小值,设函数g(x)=min{f(x),x﹣ ![]() }(x>0),若函数h(x)=g(x)﹣cx2为增函数,求实数c的取值范围.
}(x>0),若函数h(x)=g(x)﹣cx2为增函数,求实数c的取值范围.
【答案】
(1)解:函数f(x)= ![]() 的导数为f′(x)=
的导数为f′(x)= ![]() ,
,
设切点为(m,n),即有n= ![]() ,n=
,n= ![]() m,
m,
可得ame=em,①
由直线y= ![]() x为曲线y=f(x)的切线,可得
x为曲线y=f(x)的切线,可得
![]() =
= ![]() ,②
,②
由①②解得m=1,a=1;
(2)解:函数g(x)=min{f(x),x﹣ ![]() }(x>0),
}(x>0),
由f(x)= ![]() 的导数为f′(x)=
的导数为f′(x)= ![]() ,
,
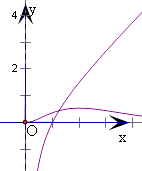
当0<x<2时,f(x)递增,x>2时,f(x)递减.
对x﹣ ![]() 在x>0递增,设y=f(x)和y=x﹣
在x>0递增,设y=f(x)和y=x﹣ ![]() 的交点为(x0,y0),
的交点为(x0,y0),
由f(1)﹣(1﹣1)= ![]() >0,f(2)﹣(2﹣
>0,f(2)﹣(2﹣ ![]() )=
)= ![]() ﹣
﹣ ![]() <0,即有1<x0<2,
<0,即有1<x0<2,
当0<x<x0时,g(x)=x﹣ ![]() ,
,
h(x)=g(x)﹣cx2=x﹣ ![]() ﹣cx2,h′(x)=1+
﹣cx2,h′(x)=1+ ![]() ﹣2cx,
﹣2cx,
由题意可得h′(x)≥0在0<x<x0时恒成立,
即有2c≤ ![]() +
+ ![]() ,由y=
,由y= ![]() +
+ ![]() 在(0,x0)递减,
在(0,x0)递减,
可得2c≤ ![]() +
+ ![]() ①
①
当x≥x0时,g(x)= ![]() ,
,
h(x)=g(x)﹣cx2= ![]() ﹣cx2,h′(x)=
﹣cx2,h′(x)= ![]() ﹣2cx,
﹣2cx,
由题意可得h′(x)≥0在x≥x0时恒成立,
即有2c≤ ![]() ,由y=
,由y= ![]() ,可得y′=
,可得y′= ![]() ,
,
可得函数y在(3,+∞)递增;在(x0,3)递减,
即有x=3处取得极小值,且为最小值﹣ ![]() .
.
可得2c≤﹣ ![]() ②,
②,
由①②可得2c≤﹣ ![]() ,解得c≤﹣
,解得c≤﹣ ![]() .
.
【解析】(1)求出f(x)的导数,设出切点(m,n),可得切线的斜率,由切线方程可得a,m的方程,解方程可得a=1;(2)y=f(x)和y=x﹣ ![]() 的交点为(x0 , y0),分别画出y=f(x)和y=x﹣
的交点为(x0 , y0),分别画出y=f(x)和y=x﹣ ![]() 在x>0的图象,可得1<x0<2,再由新定义求得最小值,求得h(x)的解析式,由题意可得h′(x)≥0在0<x<x0时恒成立,运用参数分离和函数的单调性,即可得到所求c的范围.
在x>0的图象,可得1<x0<2,再由新定义求得最小值,求得h(x)的解析式,由题意可得h′(x)≥0在0<x<x0时恒成立,运用参数分离和函数的单调性,即可得到所求c的范围.


科目:高中数学 来源: 题型:
【题目】甲,乙两人进行围棋比赛,共比赛2n(n∈N+)局,根据以往比赛胜负的情况知道,每局甲胜的概率和乙胜的概率均为 ![]() .如果某人获胜的局数多于另一人,则此人赢得比赛.记甲赢得比赛的概率为P(n).
.如果某人获胜的局数多于另一人,则此人赢得比赛.记甲赢得比赛的概率为P(n).
(1)求P(2)与P(3)的值;
(2)试比较P(n)与P(n+1)的大小,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在等腰梯形ABCD中,AB=2,CD=4,BC= ![]() ,点E,F分别为AD,BC的中点.如果对于常数λ,在ABCD的四条边上,有且只有8个不同的点P使得
,点E,F分别为AD,BC的中点.如果对于常数λ,在ABCD的四条边上,有且只有8个不同的点P使得 ![]() =λ成立,那么实数λ的取值范围为 .
=λ成立,那么实数λ的取值范围为 . 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知非空集合M满足M{0,1,2,…,n}(n≥2,n∈N+).若存在非负整数k(k≤n),使得当a∈M时,均有2k﹣a∈M,则称集合M具有性质P.设具有性质P的集合M的个数为f(n).
(1)求f(2)的值;
(2)求f(n)的表达式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,以原点O为顶点,以y轴为对称轴的抛物线E的焦点为F(0,1),点M是直线l:y=m(m<0)上任意一点,过点M引抛物线E的两条切线分别交x轴于点S,T,切点分别为B,A.
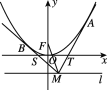
(1)求抛物线E的方程;
(2)求证:点S,T在以FM为直径的圆上.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,A,B,C的对边分别是a,b,c,3sin2C+8sin2A=11sinAsinC,且c<2a.
(1)求证:△ABC为等腰三角形
(2)若△ABC的面积为8 ![]() .且sinB=
.且sinB= ![]() ,求BC边上的中线长.
,求BC边上的中线长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某居民区随机抽取10个家庭,获得第i个家庭的月收入xi(单位:千元)与月储蓄yi(单位:千元)的数据资料,算得![]() =80,
=80, ![]() =20,
=20, ![]() =184,
=184, ![]() =720.
=720.
(1)求家庭的月储蓄y对月收入x的线性回归方程y=bx+a;
(2)判断变量x与y之间是正相关还是负相关;
(3)若该居民区某家庭月收入为7千元,预测该家庭的月储蓄.
附:线性回归方程y=bx+a中,  ,a=
,a=![]() -b
-b![]() ,其中
,其中![]() ,
, ![]() 为样本平均值.
为样本平均值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com