
【题目】已知函数f(x)= ![]() sinωx﹣
sinωx﹣ ![]() cosωx(ω<0),若y=f(x+
cosωx(ω<0),若y=f(x+ ![]() )的图象与y=f(x﹣
)的图象与y=f(x﹣ ![]() )的图象重合,记ω的最大值为ω0 , 函数g(x)=cos(ω0x﹣
)的图象重合,记ω的最大值为ω0 , 函数g(x)=cos(ω0x﹣ ![]() )的单调递增区间为( )
)的单调递增区间为( )
A.[﹣ ![]() π+
π+ ![]() ,﹣
,﹣ ![]() +
+ ![]() ](k∈Z)
](k∈Z)
B.[﹣ ![]() +
+ ![]() ,
, ![]() +
+ ![]() ](k∈Z)
](k∈Z)
C.[﹣ ![]() π+2kπ,﹣
π+2kπ,﹣ ![]() +2kπ](k∈Z)
+2kπ](k∈Z)
D.[﹣ ![]() +2kπ,﹣
+2kπ,﹣ ![]() +2kπ](k∈Z)
+2kπ](k∈Z)
科目:高中数学 来源: 题型:
【题目】如图,四棱锥 ![]() 中,底面
中,底面 ![]() 为梯形,
为梯形, ![]() 底面
底面 ![]() ,
, ![]() .过
.过 ![]() 作一个平面
作一个平面 ![]() 使得
使得 ![]() 平面
平面 ![]() .
.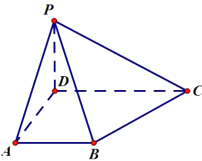
(1)求平面 ![]() 将四棱锥
将四棱锥 ![]() 分成两部分几何体的体积之比;
分成两部分几何体的体积之比;
(2)若平面 ![]() 与平面
与平面 ![]() 之间的距离为
之间的距离为 ![]() ,求直线
,求直线 ![]() 与平面
与平面 ![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某旅游爱好者计划从3个亚洲国家 ![]() 和3个欧洲国家
和3个欧洲国家 ![]() 中选择2个国家去旅游.
中选择2个国家去旅游.
(Ⅰ)若从这6个国家中任选2个,求这2个国家都是亚洲国家的概率;
(Ⅱ)若从亚洲国家和欧洲国家中各任选1个,求这2个国家包括 ![]() 但不包括
但不包括 ![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学从高三男生中随机抽取100名学生,将他们的身高数据进行整理,得到下侧的频率分布表.
组号 | 分组 | 频率 |
第1组 | [160,165) | 0.05 |
第2组 |
| 0.35 |
第3组 |
| 0.3 |
第4组 |
| 0.2 |
第5组 |
| 0.1 |
合计 | 1.00 | |
(Ⅰ)为了能对学生的体能做进一步了解,该校决定在第3,4,5组中用分层抽样的方法抽取6名学生进行体能测试,问第3,4,5组每组各应抽取多少名学生进行测试;
(Ⅱ)在(Ⅰ)的前提下,学校决定在6名学生中随机抽取2名学生进行引体向上测试,求第3组中至少有一名学生被抽中的概率;
(Ⅲ)试估计该中学高三年级男生身高的中位数位于第几组中,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆 ![]() 的方程为
的方程为 ![]() ,直线
,直线 ![]() 的方程为
的方程为 ![]() ,点
,点 ![]() 在直线
在直线 ![]() 上,过点
上,过点 ![]() 作圆
作圆 ![]() 的切线
的切线 ![]() ,切点为
,切点为 ![]() .
.
(1)若点 ![]() 的坐标为
的坐标为 ![]() ,求切线
,求切线 ![]() 的方程;
的方程;
(2)求四边形 ![]() 面积的最小值;
面积的最小值;
(3)求证:经过 ![]() 三点的圆必过定点,并求出所有定点坐标.
三点的圆必过定点,并求出所有定点坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为调查高一、高二学生周日在家学习用时情况,随机抽取了高一、高二各![]() 人,对他们的学习时间进行了统计,分别得到了高一学生学习时间(单位:小时)的频数分布表和高二学生学习时间的频率分布直方图.
人,对他们的学习时间进行了统计,分别得到了高一学生学习时间(单位:小时)的频数分布表和高二学生学习时间的频率分布直方图.
高一学生学习时间的频数分布表(学习时间均在区间![]() 内):
内):
学习时间 |
|
|
|
|
|
|
频数 | 3 | 1 | 8 | 4 | 2 | 2 |
高二学生学习时间的频率分布直方图:
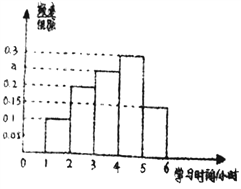
(1)求高二学生学习时间的频率分布直方图中的![]() 值,并根据此频率分布直方图估计该校高二学生学习时间的中位数;
值,并根据此频率分布直方图估计该校高二学生学习时间的中位数;
(2)利用分层抽样的方法,从高一学生学习时间在![]() ,
,![]() 的两组里随机抽取
的两组里随机抽取![]() 人,再从这
人,再从这![]() 人中随机抽取
人中随机抽取![]() 人,求学习时间在
人,求学习时间在![]() 这一组中至少有
这一组中至少有![]() 人被抽中的概率.
人被抽中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f(x),f(0)=-2,且对 ![]() ,y
,y ![]() R,都有f(x+y)-f(y)=(x+2y+1)x.
R,都有f(x+y)-f(y)=(x+2y+1)x.
(1)求f(x)的表达式;
(2)已知关于x的不等式f(x)-ax+a+1 ![]() 的解集为A,若A[2,3],求实数a的取值范围;
的解集为A,若A[2,3],求实数a的取值范围;
(3)已知数列{ ![]() }中,
}中, ![]() ,
, ![]() ,记
,记 ![]() ,且数列{
,且数列{ ![]() 的前n项和为
的前n项和为 ![]() ,
,
求证: ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com