
ЁОЬтФПЁПЫцзХЯжДњЕчзгММЪѕЕФбИУЭЗЂеЙЃЌЙигкдЊМўКЭЯЕЭГПЩППадЕФбаОПвбЗЂеЙГЩЮЊвЛУХаТЕФбЇПЦЁЊЁЊПЩППадРэТлЃЎдкПЩППадРэТлжаЃЌвЛИідЊМўе§ГЃЙЄзїЕФИХТЪГЦЮЊИУдЊМўЕФПЩППадЃЎдЊМўзщГЩЯЕЭГЃЌЯЕЭГе§ГЃЙЄзїЕФИХТЪГЦЮЊИУЯЕЭГЕФПЩППадЃЎЯжга![]() ЃЈ
ЃЈ![]() ЃЌ
ЃЌ![]() ЃЉжжЕчзгдЊМўЃЌУПжж2ИіЃЌУПИідЊМўЕФПЩППадОљЮЊ
ЃЉжжЕчзгдЊМўЃЌУПжж2ИіЃЌУПИідЊМўЕФПЩППадОљЮЊ![]() ЃЈ
ЃЈ![]() ЃЉЃЎЕБФГдЊМўВЛФме§ГЃЙЄзїЪБЃЌИУдЊМўдкЕчТЗжаНЋаЮГЩЖЯТЗЃЎЯжвЊгУет
ЃЉЃЎЕБФГдЊМўВЛФме§ГЃЙЄзїЪБЃЌИУдЊМўдкЕчТЗжаНЋаЮГЩЖЯТЗЃЎЯжвЊгУет![]() ИідЊМўзщГЩвЛИіЕчТЗЯЕЭГЃЌгаШчЯТСНжжСЌНгЗНАИПЩЙЉбЁдёЃЌЕБЧвНіЕБДгAЕНBЕФЕчТЗЮЊЭЈТЗзДЬЌЪБЃЌЯЕЭГе§ГЃЙЄзїЃЎ
ИідЊМўзщГЩвЛИіЕчТЗЯЕЭГЃЌгаШчЯТСНжжСЌНгЗНАИПЩЙЉбЁдёЃЌЕБЧвНіЕБДгAЕНBЕФЕчТЗЮЊЭЈТЗзДЬЌЪБЃЌЯЕЭГе§ГЃЙЄзїЃЎ
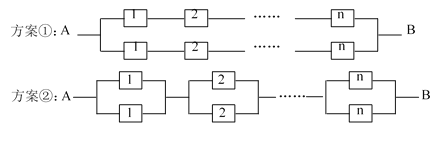
ЃЈ1ЃЉЃЈiЃЉЗжБ№аДГіАДЗНАИЂйКЭЗНАИЂкНЈСЂЕФЕчТЗЯЕЭГЕФПЩППад![]() ЁЂ
ЁЂ![]() ЃЈгУ
ЃЈгУ![]() КЭ
КЭ![]() БэЪОЃЉЃЛ
БэЪОЃЉЃЛ
ЃЈiiЃЉБШНЯ![]() гы
гы![]() ЕФДѓаЁЃЌЫЕУїФФжжСЌНгЗНАИИќЮШЖЈПЩППЃЛ
ЕФДѓаЁЃЌЫЕУїФФжжСЌНгЗНАИИќЮШЖЈПЩППЃЛ
ЃЈ2ЃЉЩш![]() ЃЌ
ЃЌ![]() ЃЌвбжЊАДЗНАИЂкНЈСЂЕФЕчТЗЯЕЭГПЩвде§ГЃЙЄзїЃЌМЧДЫЪБЯЕЭГжаЫ№ЛЕЕФдЊМўИіЪ§ЮЊ
ЃЌвбжЊАДЗНАИЂкНЈСЂЕФЕчТЗЯЕЭГПЩвде§ГЃЙЄзїЃЌМЧДЫЪБЯЕЭГжаЫ№ЛЕЕФдЊМўИіЪ§ЮЊ![]() ЃЌЧѓЫцЛњБфСП
ЃЌЧѓЫцЛњБфСП![]() ЕФЗжВМСаКЭЪ§бЇЦкЭћЃЎ
ЕФЗжВМСаКЭЪ§бЇЦкЭћЃЎ
ЁОД№АИЁПЃЈ1ЃЉЃЈiЃЉ![]() ЃЌ
ЃЌ![]() ЃЈiiЃЉ
ЃЈiiЃЉ![]() ЃЌАДЗНАИЂкНЈСЂЕФЕчТЗЯЕЭГИќЮШЖЈПЩППЃЎЃЈ2ЃЉМћНтЮіЃЌ
ЃЌАДЗНАИЂкНЈСЂЕФЕчТЗЯЕЭГИќЮШЖЈПЩППЃЎЃЈ2ЃЉМћНтЮіЃЌ![]()
ЁОНтЮіЁП
ЃЈ1ЃЉЃЈiЃЉРћгУЖдСЂЪТМўЕФИХТЪЙЋЪНМЦЫуЃЌ![]() ИідЊМўДЎСЊЭЈТЗЕФИХТЪЪЧ
ИідЊМўДЎСЊЭЈТЗЕФИХТЪЪЧ![]() ЃЌЖј
ЃЌЖј![]() ИідЊМўВЂСЊЪБВЛЭЈЕФИХТЪЪЧ
ИідЊМўВЂСЊЪБВЛЭЈЕФИХТЪЪЧ![]() ЃЌгЩДЫПЩМЦЫуПЩМЦЫуЗНАИЂйКЭЗНАИЂкНЈСЂЕФЕчТЗЯЕЭГЕФПЩППад
ЃЌгЩДЫПЩМЦЫуПЩМЦЫуЗНАИЂйКЭЗНАИЂкНЈСЂЕФЕчТЗЯЕЭГЕФПЩППад![]() ЁЂ
ЁЂ![]() ЃЛЃЈiiЃЉзїВюКѓЙЙдьКЏЪ§
ЃЛЃЈiiЃЉзїВюКѓЙЙдьКЏЪ§![]() ЃЌРћгУЕМЪ§ПЩЕУЦфЕЅЕїадДгЖјЕУ
ЃЌРћгУЕМЪ§ПЩЕУЦфЕЅЕїадДгЖјЕУ![]() гы
гы![]() ЕФДѓаЁЃЌЕУГіНсТлЃЛ
ЕФДѓаЁЃЌЕУГіНсТлЃЛ
ЃЈ2ЃЉдкЗНАИЂкЕчТЗЯЕЭГПЩвде§ГЃЙЄзїЕФЬѕМўЯТЃЌдЊМўЫ№ЛЕЕФИХТЪЪЧЬѕМўИХТЪЃЌПЩМЦЫуБрКХЯрЭЌЕФСНИіВЂСЊдЊМўжажСЖргавЛИіЫ№ЛЕЃЌЧвгавЛИіЫ№ЛЕЕФЬѕМўИХТЪЮЊ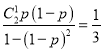 ЃЌгЩДЫПЩжЊЃЌ
ЃЌгЩДЫПЩжЊЃЌ![]() ЃЌвРДЮМЦЫуГіИїИХТЪЃЌЕУЗжВМСаЃЌдйгЩЖўЯюЗжВММЦЫуГіЦкЭћЃЎ
ЃЌвРДЮМЦЫуГіИїИХТЪЃЌЕУЗжВМСаЃЌдйгЩЖўЯюЗжВММЦЫуГіЦкЭћЃЎ
НтЃКЃЈ1ЃЉЃЈiЃЉАДЗНАИЂйНЈСЂЕФЕчТЗЯЕЭГЕФПЩППад![]() ЃЛ
ЃЛ
АДЗНАИЂкНЈСЂЕФЕчТЗЯЕЭГЕФПЩППадЮЊ![]() ЃЛ
ЃЛ
ЃЈiiЃЉ![]() ЃЎ
ЃЎ
Сю![]() ЃЌ
ЃЌ![]() Чв
Чв![]() ЃЌдђ
ЃЌдђ![]() ЃЎ
ЃЎ
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌДгЖј
ЃЌДгЖј![]() ЃЌЫљвд
ЃЌЫљвд![]() дк
дк![]() ЩЯЕЅЕїЕндіЃЛ
ЩЯЕЅЕїЕндіЃЛ
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌМД
ЃЌМД![]() ЃЎ
ЃЎ
ЫљвдЃЌ![]() ЃЌАДЗНАИЂкНЈСЂЕФЕчТЗЯЕЭГИќЮШЖЈПЩППЃЎ
ЃЌАДЗНАИЂкНЈСЂЕФЕчТЗЯЕЭГИќЮШЖЈПЩППЃЎ
ЃЈ2ЃЉдкЗНАИЂкЕчТЗЯЕЭГПЩвде§ГЃЙЄзїЕФЬѕМўЯТЃЌБрКХЯрЭЌЕФСНИіВЂСЊдЊМўжажСЖргавЛИіЫ№ЛЕЃЌЧвгавЛИіЫ№ЛЕЕФЬѕМўИХТЪЮЊ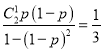 ЃЌгЩДЫПЩжЊЃЌ
ЃЌгЩДЫПЩжЊЃЌ![]() ЃЎ
ЃЎ
![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ![]() ЃЛ
ЃЛ
ЫљвдЃЌЫцЛњБфСП![]() ЕФЗжВМСаЮЊ
ЕФЗжВМСаЮЊ
| 0 | 1 | 2 | 3 | 4 |
|
|
|
|
|
|
![]() ЃЎ
ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() ЃЌЦфжаeЮЊздШЛЖдЪ§ЕФЕзЪ§.
ЃЌЦфжаeЮЊздШЛЖдЪ§ЕФЕзЪ§.
ЃЈ1ЃЉШєКЏЪ§![]() ЕФМЋаЁжЕЮЊ
ЕФМЋаЁжЕЮЊ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ2ЃЉШє![]() ЃЌжЄУїЃКЕБ
ЃЌжЄУїЃКЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ГЩСЂ.
ГЩСЂ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕxOyжаЃЌвбжЊЖЈЕуFЃЈ1ЃЌ0ЃЉЃЌЕуAдкxжсЕФЗЧе§АыжсЩЯдЫЖЏЃЌЕуBдкyжсЩЯдЫЖЏЃЌТњзу![]() 0ЃЌAЙигкЕуBЕФЖдГЦЕуЮЊMЃЌЩшЕуMЕФЙьМЃЮЊЧњЯпC.
0ЃЌAЙигкЕуBЕФЖдГЦЕуЮЊMЃЌЩшЕуMЕФЙьМЃЮЊЧњЯпC.
ЃЈ1ЃЉЧѓCЕФЗНГЬЃЛ
ЃЈ2ЃЉвбжЊЕуGЃЈ3ЃЌЉ2ЃЉЃЌЖЏжБЯпxЃНtЃЈtЃО3ЃЉгыCЯрНЛгкPЃЌQСНЕуЃЌЧѓЙ§GЃЌPЃЌQШ§ЕуЕФдВдкжБЯпyЃНЉ2ЩЯНиЕУЕФЯвГЄЕФзюаЁжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЫФРтзЖP-ABCDжаЃЌЕзУцABCDЮЊОиаЮЃЌЦНУцPCDЁЭЦНУцABCDЃЌAB=2ЃЌBC=1ЃЌ![]() ЃЌEЮЊPBжаЕуЃЎ
ЃЌEЮЊPBжаЕуЃЎ
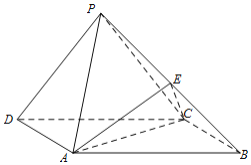
ЃЈЂёЃЉЧѓжЄЃКPDЁЮЦНУцACEЃЛ
ЃЈЂђЃЉЧѓжЄЃКPDЁЭЦНУцPBCЃЛ
ЃЈЂѓЃЉЧѓШ§РтзЖE-ABCЕФЬхЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЕуFЪЧХзЮяЯп![]() ЕФНЙЕуЃЌШєЕу
ЕФНЙЕуЃЌШєЕу![]() дкХзЮяЯпCЩЯЃЌЧв
дкХзЮяЯпCЩЯЃЌЧв![]()
ЃЈ1ЃЉЧѓХзЮяЯпCЕФЗНГЬЃЛ
ЃЈ2ЃЉЖЏжБЯп![]() гыХзЮяЯпCЯрНЛгк
гыХзЮяЯпCЯрНЛгк![]() СНЕуЃЌЮЪЃКдкxжсЩЯЪЧЗёДцдкЖЈЕу
СНЕуЃЌЮЪЃКдкxжсЩЯЪЧЗёДцдкЖЈЕу![]() ЃЈЦфжа
ЃЈЦфжа![]() ЃЉЃЌЪЙЕУxжсЦНЗж
ЃЉЃЌЪЙЕУxжсЦНЗж![]() ЃПШєДцдкЃЌЧѓГіЕуDЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЃПШєДцдкЃЌЧѓГіЕуDЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПНќФъРДЃЌЙњМвЮЊСЫЙФРјИпаЃБЯвЕЩњзджїДДвЕЃЌГіЬЈСЫаэЖргХЛнеўВпЃЌвдДДвЕДјЖЏОЭвЕЃЎФГИпаЃБЯвЕЩњаЁРюзджїДДвЕДгЪТКЃЯЪЕФХњЗЂЯњЪлЃЌЫћУПЬьвдУПЯф300дЊЕФМлИёЙКШыЛљЮЇЯКЃЌШЛКѓвдУПЯф500дЊЕФМлИёГіЪлЃЌШчЙћЕБЬьЙКШыЕФЛљЮЇЯКТєВЛЭъЃЌЪЃгрЕФОЭзїРЌЛјДІРэЃЎЮЊСЫЖдздМКЕФОгЊзДПігаИќЧхЮњЕФАбЮеЃЌЫћМЧТМСЫ150ЬьЛљЮЇЯКЕФШеЯњЪлСПЃЈЕЅЮЛЃКЯфЃЉЃЌжЦГЩШчЭМЫљЪОЕФЦЕЪ§ЗжВМЬѕаЮЭМЃЎ

ЃЈ1ЃЉШєаЁРювЛЬьЙКНј12ЯфЛљЮЇЯКЃЎ
ЂйЧѓЕБЬьЕФРћШѓ![]() ЃЈЕЅЮЛЃКдЊЃЉЙигкЕБЬьЕФЯњЪлСП
ЃЈЕЅЮЛЃКдЊЃЉЙигкЕБЬьЕФЯњЪлСП![]() ЃЈЕЅЮЛЃКЯфЃЌ
ЃЈЕЅЮЛЃКЯфЃЌ![]() ЃЉЕФКЏЪ§НтЮіЪНЃЛ
ЃЉЕФКЏЪ§НтЮіЪНЃЛ
Ђквдет150ЬьМЧТМЕФШеЯњЪлСПЕФЦЕТЪзїЮЊИХТЪЃЌЧѓЕБЬьЕФРћШѓВЛЕЭгк1900дЊЕФИХТЪЃЛ
ЃЈ2ЃЉвдЩЯЪібљБОЪ§ОнзїЮЊОіВпЕФвРОнЃЌЫћМЦЛЎНёКѓУПЬьЙКНјЛљЮЇЯКЕФЯфЪ§ЯрЭЌЃЌВЂдкНјЛѕСПЮЊ11ЯфЃЌ12ЯфжабЁдёЦфвЛЃЌЪдАяЫћШЗЖЈНјЛѕЕФЗНАИЃЌвдЪЙЦфЫљЛёЕФШеЦНОљРћШѓзюДѓЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЭждВЙцЪЧгУРДЛЭждВЕФвЛжжЦїаЕЃЌЫќЕФЙЙдьШчЭМЫљЪОЃЌдквЛИіЪЎзжаЮЕФН№ЪєАхЩЯгаСНЬѕЛЅЯрДЙжБЕФЕМВлЃЌдкжБГпЩЯгаСНИіЙЬЖЈЕФЛЌПщAЃЌBЃЌЫќУЧПЩЗжБ№дкзнВлКЭКсВлжаЛЌЖЏЃЌдкжБГпЩЯЕФЕуMДІгУЬзЙмзАЩЯЧІБЪЃЌЪЙжБГпзЊЖЏвЛжмЃЌдђЕуMЕФЙьМЃCЪЧвЛИіЭждВЃЌЦфжа|MA|ЃН2ЃЌ|MB|ЃН1ЃЌШчЭМЃЌвдСНЬѕЕМВлЕФНЛЕуЮЊдЕуOЃЌКсВлЫљдкжБЯпЮЊxжсЃЌНЈСЂжБНЧзјБъЯЕ.
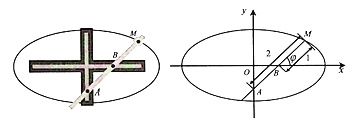
ЃЈ1ЃЉНЋвдЩфЯпBxЮЊЪМБпЃЌЩфЯпBMЮЊжеБпЕФНЧxBMМЧЮЊІеЃЈ0ЁмІеЃМ2ІаЃЉЃЌгУ![]() БэЪОЕуMЕФзјБъЃЌВЂЧѓГіCЕФЦеЭЈЗНГЬЃЛ
БэЪОЕуMЕФзјБъЃЌВЂЧѓГіCЕФЦеЭЈЗНГЬЃЛ
ЃЈ2ЃЉвбжЊЙ§CЕФзѓНЙЕуFЃЌЧвЧуаБНЧЮЊІСЃЈ0ЁмІС![]() ЃЉЕФжБЯпl1гыCНЛгкDЃЌEСНЕуЃЌЙ§ЕуFЧвДЙжБгкl1ЕФжБЯпl2гыCНЛгкGЃЌHСНЕу.ЕБ
ЃЉЕФжБЯпl1гыCНЛгкDЃЌEСНЕуЃЌЙ§ЕуFЧвДЙжБгкl1ЕФжБЯпl2гыCНЛгкGЃЌHСНЕу.ЕБ![]() ЃЌ|GH|ЃЌ
ЃЌ|GH|ЃЌ![]() вРДЮГЩЕШВюЪ§СаЪБЃЌЧѓжБЯпl2ЕФЦеЭЈЗНГЬ.
вРДЮГЩЕШВюЪ§СаЪБЃЌЧѓжБЯпl2ЕФЦеЭЈЗНГЬ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЭждВ![]() ЕФРыаФТЪЮЊ
ЕФРыаФТЪЮЊ![]() ЃЌЙ§ЖЈЕу
ЃЌЙ§ЖЈЕу![]() ЕФжБЯпlгыЭждВEЯрНЛгкAЃЌBСНЕуЃЌCЮЊЭждВЕФзѓЖЅЕуЃЌЕБжБЯпlЙ§Еу
ЕФжБЯпlгыЭждВEЯрНЛгкAЃЌBСНЕуЃЌCЮЊЭждВЕФзѓЖЅЕуЃЌЕБжБЯпlЙ§Еу![]() ЪБЃЌ
ЪБЃЌ![]() ЃЈOЮЊзјБъдЕуЃЉЕФУцЛ§ЮЊ
ЃЈOЮЊзјБъдЕуЃЉЕФУцЛ§ЮЊ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓЭждВEЕФЗНГЬЃЛ
ЃЈ2ЃЉЧѓжЄЃКЕБжБЯпlВЛЙ§CЕуЪБЃЌ![]() ЮЊЖЈжЕЃЎ
ЮЊЖЈжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЁАЬєеНВЛПЩФмЁБЕФЕчЪгНкФПЩЯЃЌМзЁЂввЁЂБћШ§ИіШЫзщГЩЕФНтУмЭХЖгВЮМгвЛЯюНтУмЬєеНЛюЖЏЃЌЙцдђЪЧгЩУмТызЈМвИјГіЬтФПЃЌШЛКѓгЩ![]() ИіШЫвРДЮГіГЁНтУмЃЌУПШЫЯоЖЈЪБМфЪЧ
ИіШЫвРДЮГіГЁНтУмЃЌУПШЫЯоЖЈЪБМфЪЧ![]() ЗжжгФкЃЌЗёдђХЩЯТвЛИіШЫ.
ЗжжгФкЃЌЗёдђХЩЯТвЛИіШЫ.![]() ИіШЫжажЛвЊгавЛШЫНтУме§ШЗЃЌдђШЯЮЊИУЭХЖгЬєеНГЩЙІЃЌЗёдђЬєеНЪЇАм.ИљОнМзвдЭљНтУмВтЪдЧщПіЃЌГщШЁСЫМз
ИіШЫжажЛвЊгавЛШЫНтУме§ШЗЃЌдђШЯЮЊИУЭХЖгЬєеНГЩЙІЃЌЗёдђЬєеНЪЇАм.ИљОнМзвдЭљНтУмВтЪдЧщПіЃЌГщШЁСЫМз![]() ДЮЕФВтЪдМЧТМЃЌЛцжЦСЫШчЯТЕФЦЕТЪЗжВМжБЗНЭМ.
ДЮЕФВтЪдМЧТМЃЌЛцжЦСЫШчЯТЕФЦЕТЪЗжВМжБЗНЭМ.
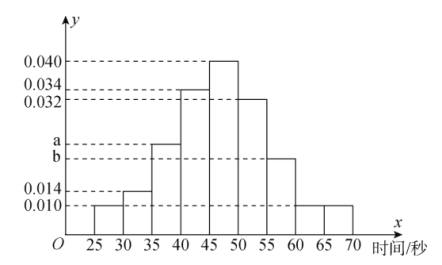
ЃЈ1ЃЉШєМзНтУмГЩЙІЫљашЪБМфЕФжаЮЛЪ§ЮЊ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЁЂ
ЁЂ![]() ЕФжЕЃЌВЂЧѓГіМздк
ЕФжЕЃЌВЂЧѓГіМздк![]() ЗжжгФкНтУмГЩЙІЕФЦЕТЪЃЛ
ЗжжгФкНтУмГЩЙІЕФЦЕТЪЃЛ
ЃЈ2ЃЉдкЁАЬєеНВЛПЩФмЁБНкФПЩЯгЩгкРДздИїЗНМАздЩэЕФаФРэбЙСІЃЌМзЃЌввЃЌБћНтУмГЩЙІЕФИХТЪЗжБ№ЮЊ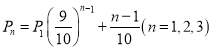 ЃЌЦфжа
ЃЌЦфжа![]() БэЪОЕк
БэЪОЕк![]() ИіГіГЁбЁЪжНтУмГЩЙІЕФИХТЪЃЌВЂЧв
ИіГіГЁбЁЪжНтУмГЩЙІЕФИХТЪЃЌВЂЧв![]() ЖЈвхЮЊМзГщбљжаНтУмГЩЙІЕФЦЕТЪДњЬцЃЌИїШЫЪЧЗёНтУмГЩЙІЯрЛЅЖРСЂ.
ЖЈвхЮЊМзГщбљжаНтУмГЩЙІЕФЦЕТЪДњЬцЃЌИїШЫЪЧЗёНтУмГЩЙІЯрЛЅЖРСЂ.
ЂйЧѓИУЭХЖгЬєеНГЩЙІЕФИХТЪЃЛ
ЂкИУЭХЖгвд![]() ДгаЁЕНДѓЕФЫГађАДХХМзЁЂввЁЂБћШ§ИіШЫЩЯГЁНтУмЃЌЧѓЭХЖгЬєеНГЩЙІЫљашХЩГіЕФШЫдБЪ§ФП
ДгаЁЕНДѓЕФЫГађАДХХМзЁЂввЁЂБћШ§ИіШЫЩЯГЁНтУмЃЌЧѓЭХЖгЬєеНГЩЙІЫљашХЩГіЕФШЫдБЪ§ФП![]() ЕФЗжВМСагыЪ§бЇЦкЭћ.
ЕФЗжВМСагыЪ§бЇЦкЭћ.
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com