
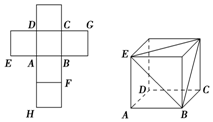
分析 (1)把正方体的平面展开图还原成正方体,能将字母F,G,H标记在正方体相应的顶点处.
(2)由AH∥BG,则∠EBG是异面直线AH与EB所成角(或所成角的补角),由此能求出异面直线AH与EB所成角.
(3)由平面ABCD∥平面EFGH,平面BEG∩平面ABCD=直线L,平面BEG∩平面EFGH=EG,得到EG∥直线L.
解答 解:(1)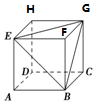 把正方体的平面展开图还原成正方体,
把正方体的平面展开图还原成正方体,
将字母F,G,H标记在正方体相应的顶点处,如右图.
(2)∵AH∥BG,∴∠EBG是异面直线AH与EB所成角(或所成角的补角),
连结EB,BG,GE,
∵EB=BG=GE,∴∠EBG=60°,
∴异面直线AH与EB所成角为60°.
(3)EG∥直线L,理由如下:
∵平面ABCD∥平面EFGH,
平面BEG∩平面ABCD=直线L,平面BEG∩平面EFGH=EG,
∴EG∥直线L.
点评 本题考查异面直线所成角的求法,考查两直线位置关系的判断,是中档题,解题时要认真审题,注意空间思维能力的培养.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com