
【题目】已知定义域为![]() 的单调递减的奇函数
的单调递减的奇函数![]() ,当
,当![]() 时,
时, ![]() .
.
(1)求![]() 的值;
的值;
(2)求![]() 的解析式;
的解析式;
(3)若对任意的![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)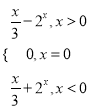 ;(3)
;(3)![]() .
.
【解析】试题分析:(1)根据函数为奇函数得![]() ,结合当
,结合当![]() 时,
时, ![]() ,即可求出
,即可求出![]() 的值;(2)由定义域为
的值;(2)由定义域为![]() 的函数
的函数![]() 是奇函数,知
是奇函数,知![]() .当
.当![]() 时,
时, ![]() ,由函数
,由函数![]() 是奇函数,知
是奇函数,知![]() ,由此能求出
,由此能求出![]() 的解析式;(3)由
的解析式;(3)由![]() 是
是![]() 上单调递减的奇函数,
上单调递减的奇函数, ![]() ,得
,得![]() 即
即![]() 恒成立,再由根的判别式小于零即可求出实数
恒成立,再由根的判别式小于零即可求出实数![]() 的取值范围.
的取值范围.
试题解析:(1)f(﹣1)=﹣f(1)=﹣(![]() ﹣2)=
﹣2)=![]() ;
;
(2)∵定义域为R的函数f(x)是奇函数,
∴f(0)=0,
当x<0时,﹣x>0,
f(﹣x)=﹣![]() ﹣2﹣x ,
﹣2﹣x ,
又∵函数f(x)是奇函数,
∴f(﹣x)=﹣f(x),
∴f(x)=![]() +2﹣x ,
+2﹣x ,
综上所述f(x)=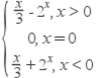 .
.
(3)∵f(1)=﹣![]() <f(0)=0,
<f(0)=0,
且f(x)在R上单调,
∴f(x)在R上单调递减,
由f(t2﹣2t)+f(2t2﹣k)<0,
得f(t2﹣2t)<﹣f(2t2﹣k),
∵f(x)是奇函数,
∴f(t2﹣2t)<f(k﹣2t2),
又∵f(x)是减函数,
∴t2﹣2t>k﹣2t2
即3t2﹣2t﹣k>0对任意t∈R恒成立,
∴△=4+12k<0得k<﹣![]() ,即为所求.
,即为所求.


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:高中数学 来源: 题型:
【题目】如图,在矩形ABCD中,已知AB=a,BC=b(a>b),在AB,AD,CB,CD上,分别截取AE=AH=CF=CG=x(x>0),设四边形EFGH的面积为y.
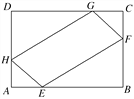
(1)写出四边形EFGH的面积y与x之间的函数关系;
(2)求当x为何值时y取得最大值,最大值是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2014年5月,我省南昌市遭受连日大暴雨天气,某网站就“民众是否支持加大修建城市地下排水设施的资金投入”进行投票,按照南昌暴雨前后两个时间收集有效投票,暴雨后的投票收集了![]() 份,暴雨前的投票也收集了
份,暴雨前的投票也收集了![]() 份,所得统计结果如下表:
份,所得统计结果如下表:

已知工作人与从所有投票中任取一个,取到“不支持投入”的投票的概率为![]() .
.
(1)求列表中数据的值;
(2)能够有多大的把握认为南昌暴雨对民众是否赞成加大对修建城市地下排水设施的投入有关系?
附: 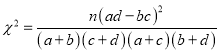
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() 的右焦点为F,右顶点为A,设离心率为e,且满足
的右焦点为F,右顶点为A,设离心率为e,且满足![]() ,其中O为坐标原点.
,其中O为坐标原点.
(Ⅰ)求椭圆C的方程;
(Ⅱ)过点![]() 的直线l与椭圆交于M,N两点,求△OMN面积的最大值.
的直线l与椭圆交于M,N两点,求△OMN面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=xlnx,g(x)=x3+ax2-x+2.
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)对任意x∈(0,+∞),![]() 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com