练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

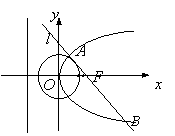
    （08年东北师大附中）（12分）

    已知是抛物线的焦点，过的直线与圆： 切于点 .

    (Ⅰ) 求抛物线的方程;

    (Ⅱ) 若与抛物线交于两点，在直线：上，点在圆上，求当时，△面积的最大值.

    解析：（Ⅰ）把代入中得：，解得：

    即所以由直线与圆切于点得直线的方程是

    令则所以.可得抛物线的方程是………………5分

    (Ⅱ)作，则

    因为由已知，

    且由抛物线的定义可知

    所以当时，成立.

    由

    解得:

    这时,, 作垂足,所以三角形的面积所以当最大时,三角形面积最大,这时可得点的位置是圆与轴的右交点,的最大值等于……………12分

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    （08年东北师大附中三摸理） （12分） 在数列中，，，记，.

    （Ⅰ）证明：数列是等比数列；

    （Ⅱ）记，数列的前n项和为，求证：．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

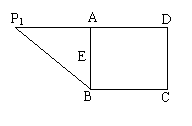
    （08年东北师大附中三摸理） （12分）如图，在直角梯形P1DCB中，P1D∥CB，CD⊥P1D，P1D＝6，BC＝3，DC＝，A是P1D的中点，E是线段AB的中点，沿AB把平面P1AB折起到平面PAB的位置，使二面角P－CD－B成45°角．

       （Ⅰ）求证：PA⊥平面ABCD；

       （Ⅱ）求平面PEC和平面PAD所成的锐二面角的大小．

                               

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （08年东北师大附中四摸文）  已知函数的图象为曲线.

    (Ⅰ) 若曲线上存在点，使曲线在点处的切线与轴平行，求的关系；

    (Ⅱ) 说明函数可以在和时取得极值，并求此时的值；

    (Ⅲ) 在满足(2)的条件下，在时恒成立，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （08年东北师大附中四摸）（12分）已知双曲线的中心在原点，对称轴为坐标轴，其一条渐近线方程是，且双曲线过点.

    (1)     求此双曲线的方程；

    (2)     设直线过点，其方向向量为，令向量满足.双曲线的右支上是否存在唯一一点，使得. 若存在，求出对应的值和的坐标；若不存在，说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （08年东北师大附中理）（12分）

     

        某市举行的一次数学新课程骨干教师培训，共邀请10名使用不同版本教材的教师，数据如下表所示：

     

    版本

    人教A版

    人教B版

    性别

    男教师

    女教师

    男教师

    女教师

    人数

    3

    2

    2

    3

    （Ⅰ）从这10名教师中随机选出2名，则2人恰好是教不同版本的男教师的概率是多少？

    （Ⅱ）培训活动随机选出2名代表发言，设发言代表中使用人教B版的女教师人数为，求随机变量的分布列和数学期望．

    查看答案和解析>>

    同步练习册答案