
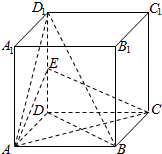
 如图,在正方体ABCD-A1B1C1D1中,E为DD1的中点.
如图,在正方体ABCD-A1B1C1D1中,E为DD1的中点.分析 (Ⅰ)连接BD交AC于F,连EF.可证EF∥D1B,又EF?平面EAC,从而可求得BD1∥平面EAC.
(Ⅱ)先证明AC⊥BD,有DD1⊥平面ABCD,又AC?平面ABCD,可证明DD1⊥AC,从而可证AC⊥平面D1DB,即证明平面D1DB⊥平面AEC.
解答  证明:(Ⅰ)BD交AC于F,连EF,
证明:(Ⅰ)BD交AC于F,连EF,
因为F为正方形ABCD对角线的交点,
所长F为AC、BD的中点,
在DD1B中,E、F分别为DD1、DB的中点,
所以EF∥D1B,
又EF?平面EAC,所以BD1∥平面EAC;
(Ⅱ)在正方体ABCD-A1B1C1D1中,
∵四边形ABCD是正方形,∴AC⊥BD
又在正方体ABCD-A1B1C1D1中,
∵DD1⊥平面ABCD,
又AC?平面ABCD,∴DD1⊥AC
DD1?平面D1DB,BD?平面D1DB,BD∩DD1=D
∴AC⊥平面D1DB
∵AC?平面AEC,
∴平面D1DB⊥平面AEC.
点评 本题主要考查平面与平面垂直的判定,直线与平面平行的判定,考查了转化思想,综合性较强,属于中档题.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既非充分又非必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $3-2\sqrt{2}$ | B. | $-3+2\sqrt{2}$ | C. | $-3±2\sqrt{2}$ | D. | $3±2\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
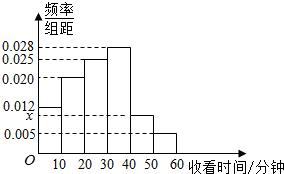 某电视传媒公司为了了解某类体育节目的收视情况,随机抽取了100名观众进行调查,如图是根据调查结果绘制的观众日均收看该类体育节目时间的频率分布直方图,其中收看时间分组区间是:[0,10),[10,20),[20,30),[30,40),[40,50),[50,60].则图中x的值为0.01.
某电视传媒公司为了了解某类体育节目的收视情况,随机抽取了100名观众进行调查,如图是根据调查结果绘制的观众日均收看该类体育节目时间的频率分布直方图,其中收看时间分组区间是:[0,10),[10,20),[20,30),[30,40),[40,50),[50,60].则图中x的值为0.01.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com