
【题目】已知函数f(x)是定义在R上的奇函数,且当x≥0时f(x)= ![]() .
.
(1)求f(x)的解析式;
(2)判断f(x)的单调性(不必证明);
(3)若对任意的t∈R,不等式f(k﹣3t2)+f(t2+2t)≤0恒成立,求k的取值范围.
【答案】
(1)
解:∵当x≥0时有 ![]() ,
,
∴当x≤0时,﹣x≥0,
![]()
∴ ![]() (x≤0),
(x≤0),
∴ 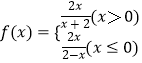
(2)
解:∵当x≥0时有 ![]() ,∴f(x)在[0,+∞)上是增函数
,∴f(x)在[0,+∞)上是增函数
又∵f(x)是奇函数,∴f(x)是在(﹣∞,+∞)上是增函数
(注:只判断f(x)是在(﹣∞,+∞)上是增函数)
(3)
解:f(k﹣3t2)+f(t2+2t)≤0则f(t2+2t)≤﹣f(k﹣3t2)=f(3t2﹣k)
因f(x)为增函数,由上式推得,t2+2t≤3t2﹣k,∴2t2﹣2t﹣k≥0
即对一切t∈R恒有2t2﹣2t﹣k≥0
从而判别式△=4+8k≤0,∴ ![]()
【解析】(1)依题意,当x≤0时,﹣x≥0,利用 ![]() ,可求得当x≤0时的函数表达式,从而可得f(x)的解析式;(2)当x≥0时,将函数
,可求得当x≤0时的函数表达式,从而可得f(x)的解析式;(2)当x≥0时,将函数 ![]() 分离出常数2,利用反比例函数的单调性可判断出f(x)在[0,+∞)上是增函数,再利用奇函数的单调性质,可判断f(x)的单调性;(3)利用(2)可知,f(x)在(﹣∞,+∞)上是增函数,再利用奇函数的性质,将不等式f(k﹣3t2)+f(t2+2t)≤0转化为t2+2t≤3t2﹣k恒成立,利用判别式△=4+8k≤0即可求得k的取值范围.
分离出常数2,利用反比例函数的单调性可判断出f(x)在[0,+∞)上是增函数,再利用奇函数的单调性质,可判断f(x)的单调性;(3)利用(2)可知,f(x)在(﹣∞,+∞)上是增函数,再利用奇函数的性质,将不等式f(k﹣3t2)+f(t2+2t)≤0转化为t2+2t≤3t2﹣k恒成立,利用判别式△=4+8k≤0即可求得k的取值范围.
【考点精析】解答此题的关键在于理解函数的单调性的相关知识,掌握注意:函数的单调性是函数的局部性质;函数的单调性还有单调不增,和单调不减两种.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() :
: ![]() ,曲线
,曲线![]() :
: ![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点, ![]() 轴正半轴为极轴,建立极坐标系.
轴正半轴为极轴,建立极坐标系.
(Ⅰ)求曲线![]() ,
, ![]() 的极坐标方程;
的极坐标方程;
(Ⅱ)曲线![]() :
: ![]() (
(![]() 为参数,
为参数, ![]() ,
, ![]() )分别交
)分别交![]() ,
, ![]() 于
于![]() ,
, ![]() 两点,当
两点,当![]() 取何值时,
取何值时, ![]() 取得最大值.
取得最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知: ![]() 、
、 ![]() 、
、 ![]() 是同一平面上的三个向量,其中
是同一平面上的三个向量,其中 ![]() =(1,2).
=(1,2).
(1)若| ![]() |=2
|=2 ![]() ,且
,且 ![]() ∥
∥ ![]() ,求
,求 ![]() 的坐标.
的坐标.
(2)若| ![]() |=
|= ![]() ,且
,且 ![]() +2
+2 ![]() 与2
与2 ![]() ﹣
﹣ ![]() 垂直,求
垂直,求 ![]() 与
与 ![]() 的夹角θ
的夹角θ
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a1=3,an=2an﹣1+(t+1)2n+3m+t(t,m∈R,n≥2,n∈N*)
(1)t=0,m=0时,求证: ![]() 是等差数列;
是等差数列;
(2)t=﹣1,m= ![]() 是等比数列;
是等比数列;
(3)t=0,m=1时,求数列{an}的通项公式和前n项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某社区工会对当地企业工人月收入情况进行一次抽样调查后画出的频率分布直方图,其中第二组月收入在[1.5,2)千元的频数为300,则此次抽样的样本容量为( ) 
A.1000
B.2000
C.3000
D.4000
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一次测验共有4个选择题和2个填空题,每答对一个选择题得20分,每答对一个填空题得10分,答错或不答得0分,若某同学答对每个选择题的概率均为 ![]() ,答对每个填空题的概率均为
,答对每个填空题的概率均为 ![]() ,且每个题答对与否互不影响.
,且每个题答对与否互不影响.
(1)求该同学得80分的概率;
(2)若该同学已经答对了3个选择题和1个填空题,记他这次测验的得分为ξ,求ξ的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知空间四边形ABCD的两条对角线的长AC=6,BD=8,AC与BD所成的角为30o , E,F,G,H分别是AB,BC,CD,DA的中点,求四边形EFGH的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
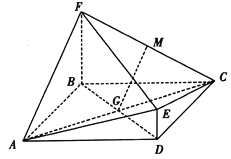
【题目】如图,菱![]() 与四边形BDEF相交于BD,
与四边形BDEF相交于BD, ![]() 平面ABCD,DE//BF,BF=2DE,AF⊥FC,M为CF的中点,
平面ABCD,DE//BF,BF=2DE,AF⊥FC,M为CF的中点, ![]() .
.
(I)求证:GM//平面CDE;
(II)求证:平面ACE⊥平面ACF.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com