
分析 由题意可得$\overrightarrow{a}•\overrightarrow{b}$=0,代值计算即可.
解答 解:∵${|{\overrightarrow a+\overrightarrow b}|^2}={|{\overrightarrow a}|^2}+{|{\overrightarrow b}|^2}$,
∴$\overrightarrow{a}•\overrightarrow{b}$=0,
∵向量$\overrightarrow a=(m,1)$,$\overrightarrow b=(1,2)$,
∴m+2=0,
解得,m=-2,
故答案为:-2;
点评 本题考查了向量的垂直和向量的数量的运算,属于基础题.


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{11π}{6}$ | D. | $\frac{5π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,+∞) | B. | (0,2) | C. | (0,2)∪(-∞,-1) | D. | (2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
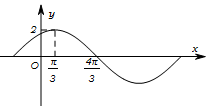 已知函数f(x)=Asin(ωx+φ).($A>0,ω>0,0<φ<\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=Asin(ωx+φ).($A>0,ω>0,0<φ<\frac{π}{2}$)的部分图象如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{4}{5}$,-$\frac{2}{5}$) | B. | (-$\frac{2}{5}$,$\frac{4}{5}$) | C. | ($\frac{4}{5}$,$\frac{2}{5}$) | D. | ($\frac{2}{5}$,-$\frac{4}{5}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 60° | C. | 120° | D. | 150° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | sinx<x,x∈(-π,π) | B. | x-x2>0,x∈(0,2) | C. | ex>1+x,x∈R | D. | lnx≤x-1,x∈(0,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{5}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com