
分析 由题意和三角函数公式可得C=120°,再由余弦定理和基本不等式可得ab的范围,再由三角形的面积公式可得.
解答 解:∵2sin2$\frac{A+B}{2}$=1+cos2C,∴1-cos(A+B)=1+cos2C,
∴1+cosC=1+cos2C,∴cosC=2cos2C-1,
解得cosC=$-\frac{1}{2}$或cosC=1,
∵C为三角形内角,∴cosC=$-\frac{1}{2}$,∴C=120°,
∴由余弦定理可得3=a2+b2-2abcosC=a2+b2+ab,
由基本不等式可得3=a2+b2+ab≥2ab+ab=3ab,
∴ab≤1,当且仅当a=b时取等号,
∴△ABC面积S=$\frac{1}{2}$absinC=$\frac{\sqrt{3}}{4}$ab≤$\frac{\sqrt{3}}{4}$,
故答案为:(0,$\frac{\sqrt{3}}{4}$].
点评 本题考查三角函数恒等变换,涉及解三角形和基本不等式,属中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
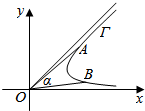 如图,在平面直角坐标系xOy中,对于曲线Γ,若存在以O为顶点的角α,使得α≥∠AOB对于曲线π上的任意两个不同的点A,B恒成立,则称角α为曲线的相对于点O的“渐近角”并称其中最小的“渐近角”为曲线Γ的相对于点O的“望角”.已知曲线C:y=$\left\{\begin{array}{l}{2x{e}^{x-1}+2,x>0}\\{\frac{\sqrt{36+25{x}^{2}}}{3},x≤0}\end{array}\right.$(其中e=2.71828…是自然对数的底数),则曲线C的相对于点O的“望角”为( )
如图,在平面直角坐标系xOy中,对于曲线Γ,若存在以O为顶点的角α,使得α≥∠AOB对于曲线π上的任意两个不同的点A,B恒成立,则称角α为曲线的相对于点O的“渐近角”并称其中最小的“渐近角”为曲线Γ的相对于点O的“望角”.已知曲线C:y=$\left\{\begin{array}{l}{2x{e}^{x-1}+2,x>0}\\{\frac{\sqrt{36+25{x}^{2}}}{3},x≤0}\end{array}\right.$(其中e=2.71828…是自然对数的底数),则曲线C的相对于点O的“望角”为( )| A. | $\frac{3π}{4}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com