
【题目】已知椭圆![]() 的上顶点到左焦点
的上顶点到左焦点![]() 的距离为
的距离为![]() .直线
.直线![]() 与椭圆
与椭圆![]() 交于不同两点
交于不同两点![]() 、
、![]() (
(![]() 、
、![]() 都在
都在![]() 轴上方),且
轴上方),且![]() .
.

(1)求椭圆![]() 的方程;
的方程;
(2)当![]() 为椭圆与
为椭圆与![]() 轴正半轴的交点时,求直线
轴正半轴的交点时,求直线![]() 方程;
方程;
(3)对于动直线![]() ,是否存在一个定点,无论
,是否存在一个定点,无论![]() 如何变化,直线
如何变化,直线![]() 总经过此定点?若存在,求出该定点的坐标;若不存在,请说明理由.
总经过此定点?若存在,求出该定点的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)直线
;(3)直线![]() 过定点
过定点![]() ,证明见解析.
,证明见解析.
【解析】
(1)设椭圆![]() 的方程为
的方程为![]() ,根据题意可求得
,根据题意可求得![]() 、
、![]() 的值,进而可得椭圆
的值,进而可得椭圆![]() 的方程;
的方程;
(2)求出直线![]() 的方程,将直线
的方程,将直线![]() 的方程与椭圆
的方程与椭圆![]() 的方程联立,求得点
的方程联立,求得点![]() 的坐标,进而可求得直线
的坐标,进而可求得直线![]() 的方程;
的方程;
(3)由题意可知,直线![]() 的斜率存在,可设直线
的斜率存在,可设直线![]() 的方程为
的方程为![]() ,设点
,设点![]() 、
、![]() ,将直线
,将直线![]() 的方程与椭圆
的方程与椭圆![]() 的方程联立,列出韦达定理,由已知条件得知直线
的方程联立,列出韦达定理,由已知条件得知直线![]() 和
和![]() 的斜率之和为
的斜率之和为![]() ,代入韦达定理化简计算得出
,代入韦达定理化简计算得出![]() 与
与![]() 所满足的关系式,进而得出直线
所满足的关系式,进而得出直线![]() 所过的定点坐标.
所过的定点坐标.
(1)设椭圆![]() 的方程为
的方程为![]() ,
,
该椭圆的上顶点到左焦点![]() 的距离为,即
的距离为,即![]() ,可得
,可得![]() ,
,![]() ,
,
因此,椭圆![]() 的方程为
的方程为![]() ;
;
(2)由题意可得![]() ,
,![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,
,
![]() ,则直线
,则直线![]() 的斜率为
的斜率为![]() ,
,
直线![]() 的方程为
的方程为![]() ,
,
联立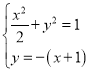 ,得
,得![]() ,解得
,解得![]() 或
或![]() ,所以点
,所以点![]() 的坐标为
的坐标为![]() .
.
直线![]() 的斜率为
的斜率为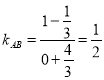 ,因此,直线
,因此,直线![]() 的方程为
的方程为![]() ;
;
(3)由于直线![]() 与椭圆
与椭圆![]() 的两交点
的两交点![]() 、
、![]() 都在
都在![]() 轴上方,则直线
轴上方,则直线![]() 的斜率存在,
的斜率存在,
设直线![]() 的方程为
的方程为![]() ,设点
,设点![]() 、
、![]() ,
,
联立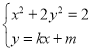 ,消去
,消去![]() 得
得![]() ,
,
![]() ,得
,得![]() ,
,
由韦达定理得![]() ,
,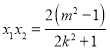 ,
,
![]() ,所以,直线
,所以,直线![]() 和
和![]() 的斜率之和为
的斜率之和为![]() ,
,
即![]()
![]() ,
,
![]() ,
,
![]() ,则直线
,则直线![]() 的方程为
的方程为![]() ,直线
,直线![]() 过定点
过定点![]() .
.


科目:高中数学 来源: 题型:
【题目】树立和践行“绿水青山就是金山银山,坚持人与自然和谐共生”的理念越来越深入人心,已形成了全民自觉参与,造福百姓的良性循环.据此,某网站推出了关于生态文明建设进展情况的调查,调查数据表明,环境治理和保护问题仍是百姓最为关心的热点,参与调查者中关注此问题的约占![]() .现从参与关注生态文明建设的人群中随机选出200人,并将这200人按年龄分组:第1组
.现从参与关注生态文明建设的人群中随机选出200人,并将这200人按年龄分组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.

(1)求出![]() 的值;
的值;
(2)现在要从年龄较小的第1,2组中用分层抽样的方法抽取5人,再从这5人中随机抽取3人进行问卷调查,求第2组恰好抽到2人的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() ,
,![]() 是离心率为
是离心率为![]() 的椭圆
的椭圆![]() 的左、右焦点,直线
的左、右焦点,直线![]() ,将线段
,将线段![]() ,
,![]() 分成两段,其长度之比为
分成两段,其长度之比为![]() ,设
,设![]() 是
是![]() 上的两个动点,线段
上的两个动点,线段![]() 的中垂线与椭圆
的中垂线与椭圆![]() 交于
交于![]() 两点,线段
两点,线段![]() 的中点
的中点![]() 在直线
在直线![]() 上.
上.

(1)求椭圆![]() 的方程;
的方程;
(2)求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公园准备在一圆形水池里设置两个观景喷泉,观景喷泉的示意图如图所示,![]() 两点为喷泉,圆心
两点为喷泉,圆心![]() 为
为![]() 的中点,其中
的中点,其中![]() 米,半径
米,半径![]() 米,市民可位于水池边缘任意一点
米,市民可位于水池边缘任意一点![]() 处观赏.
处观赏.
(1)若当![]() 时,
时,![]() ,求此时
,求此时![]() 的值;
的值;
(2)设![]() ,且
,且![]() .
.
(i)试将![]() 表示为
表示为![]() 的函数,并求出
的函数,并求出![]() 的取值范围;
的取值范围;
(ii)若同时要求市民在水池边缘任意一点![]() 处观赏喷泉时,观赏角度
处观赏喷泉时,观赏角度![]() 的最大值不小于
的最大值不小于![]() ,试求
,试求![]() 两处喷泉间距离的最小值.
两处喷泉间距离的最小值.

查看答案和解析>>
科目:高中数学 来源: 题型:
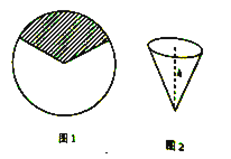
【题目】现有一张半径为![]() 的圆形铁皮,从中裁剪出一块扇形铁皮(如图
的圆形铁皮,从中裁剪出一块扇形铁皮(如图![]() 阴影部分),并卷成一个深度为
阴影部分),并卷成一个深度为![]() 的圆锥筒,如图
的圆锥筒,如图![]() .
.
(1)若所裁剪的扇形铁皮的圆心角为![]() ,求圆锥筒的容积;
,求圆锥筒的容积;
(2)当![]() 为多少时,圆锥筒的容积最大?并求出容积的最大值.
为多少时,圆锥筒的容积最大?并求出容积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com