
【题目】已知函数f(x)=2x﹣1+a,g(x)=bf(1﹣x),其中a,b∈R,若关于x的不等式f(x)≥g(x)的解的最小值为2,则实数a的取值范围是 .
【答案】a≤﹣2或a>﹣ ![]()
【解析】解:f(x)=2x﹣1+a,
g(x)=bf(1﹣x)=b(21﹣x﹣1+a)=b(2﹣x+a),
∵f(x)≥g(x),
∴2x﹣1+a≥b(2﹣x+a),
令F(x)=2x﹣1+a﹣b(2﹣x+a)= ![]() +a﹣
+a﹣ ![]() ﹣ab=
﹣ab= ![]() ﹣
﹣ ![]() +a﹣ab,
+a﹣ab,
①若b<0,则 ![]() (
( ![]() ﹣
﹣ ![]() +a﹣ab)=+∞,与关于x的不等式f(x)≥g(x)的解的最小值为2相矛盾,故不成立;
+a﹣ab)=+∞,与关于x的不等式f(x)≥g(x)的解的最小值为2相矛盾,故不成立;
②若b=0,则F(x)= ![]() ﹣
﹣ ![]() +a﹣ab在R上是增函数;即F(x)=
+a﹣ab在R上是增函数;即F(x)= ![]() +a≥0的解集为[2,+∞),a=﹣2;
+a≥0的解集为[2,+∞),a=﹣2;
③若b>0,则F(x)= ![]() ﹣
﹣ ![]() +a﹣ab在R上是增函数;即F(x)≥0的解集为[2,+∞),
+a﹣ab在R上是增函数;即F(x)≥0的解集为[2,+∞),
2+a=b( ![]() +a),b=
+a),b= ![]() >0,a<﹣2或a>﹣
>0,a<﹣2或a>﹣ ![]() ;综上所述,a≤﹣2或a>﹣
;综上所述,a≤﹣2或a>﹣ ![]() ,
,
所以答案是:a≤﹣2或a>﹣ ![]() .
.
【考点精析】本题主要考查了指数函数的图像与性质的相关知识点,需要掌握a0=1, 即x=0时,y=1,图象都经过(0,1)点;ax=a,即x=1时,y等于底数a;在0<a<1时:x<0时,ax>1,x>0时,0<ax<1;在a>1时:x<0时,0<ax<1,x>0时,ax>1才能正确解答此题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,设圆弧x2+y2=1(x≥0,y≥0)与两坐标轴正半轴围成的扇形区域为M,过圆弧上中点A做该圆的切线与两坐标轴正半轴围成的三角形区域为N.现随机在区域N内投一点B,若设点B落在区域M内的概率为P,则P的值为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,有一块矩形空地,要在这块空地上开辟一个内接四边形为绿地,使其四个顶点分别落在矩形的四条边上,已知AB=a(a>2),BC=2,且AE=AH=CF=CG,设AE=x,绿地面积为y.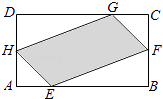
(1)写出y关于x的函数关系式,并指出这个函数的定义域;
(2)当AE为何值时,绿地面积y最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直角三角形ABC的顶点坐标A(﹣2,0),直角顶点 ![]() ,顶点C在x轴上,点P为线段OA的中点. (Ⅰ)求BC边所在直线方程;
,顶点C在x轴上,点P为线段OA的中点. (Ⅰ)求BC边所在直线方程;
(Ⅱ)圆M是△ABC的外接圆,求圆M的方程.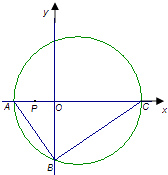
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)=x2﹣2ax+1,a∈R;
(1)若函数f(x)在区间(﹣1,2)上是单调函数,求实数a的取值范围;
(2)若不等式f(x)>0对任x∈R上恒成立,求实数a的取值范围;
(3)若函数f(x)在区间[1,+∞)的最小值为﹣2,求实数a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设抛物线y2=2px(p>0)的焦点为F,其准线与x轴的交点为Q,过Q点的直线l交抛物线于A,B两点.
(1)若直线l的斜率为 ![]() ,求证:
,求证: ![]() ;
;
(2)设直线FA,FB的斜率分别为k1 , k2 , 求k1+k2的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() (a>b>0)的左焦点为F(﹣2,0),离心率为
(a>b>0)的左焦点为F(﹣2,0),离心率为 ![]() . (Ⅰ)求椭圆C的标准方程;
. (Ⅰ)求椭圆C的标准方程;
(Ⅱ)设O为坐标原点,T为直线x=﹣3上一点,过F作TF的垂线交椭圆于P、Q,当四边形OPTQ是平行四边形时,求四边形OPTQ的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com