
【题目】如甲图所示,在矩形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() 是
是![]() 的中点,将
的中点,将![]() 沿
沿![]() 折起到
折起到![]() 位置,使平面
位置,使平面![]() 平面
平面![]() ,得到乙图所示的四棱锥
,得到乙图所示的四棱锥![]() .
.
(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值.
的余弦值.
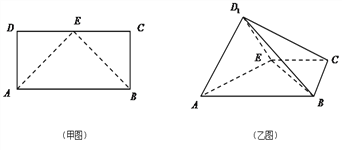
【答案】(Ⅰ)见解析;(Ⅱ) ![]() .
.
【解析】试题分析:(Ⅰ)取![]() 中点
中点![]() ,连
,连![]() ,证得
,证得![]() ,又
,又![]() 平面
平面![]() 平面
平面![]() ,证得
,证得![]() 平面
平面![]() ,证明
,证明![]() 再利用线面的判定定理,即可证得
再利用线面的判定定理,即可证得![]() 平面
平面![]()
(Ⅱ)由题意,取![]() 中点
中点![]() ,以
,以![]() 为坐标原点,分别以
为坐标原点,分别以![]() ,
, ![]() 为
为![]() 轴正方向建立空间直角坐标系
轴正方向建立空间直角坐标系![]() ,由(Ⅰ)知:
,由(Ⅰ)知: ![]() 是平面
是平面![]() 的法向量,设平面
的法向量,设平面![]() 的法向量为
的法向量为![]() ,利用空间向量的夹角公式,即可求解结论.
,利用空间向量的夹角公式,即可求解结论.
试题解析:
(Ⅰ)如下图,取![]() 中点
中点![]() ,连
,连![]() ,在
,在![]() 中,
中, ![]() ,
, ![]() ,又
,又![]() 平面
平面![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
, ![]() ,即
,即![]() .在
.在![]() 中,易得
中,易得![]() ,
, ![]() ,
, ![]() ,
,
![]() ,又
,又![]() ,
,
![]() 平面
平面![]()

(Ⅱ)由题意,取![]() 中点
中点![]() ,以
,以![]() 为坐标原点,分别以
为坐标原点,分别以![]() ,
, ![]() 为
为![]() 轴正方向建立间直角坐标系
轴正方向建立间直角坐标系![]() 如图所示,则
如图所示,则![]() ,由(Ⅰ)知:
,由(Ⅰ)知: ![]() 是平面
是平面![]() 的法向量,设平面
的法向量,设平面![]() 的法向量为
的法向量为![]() ,则
,则
 ,令
,令![]() ,则
,则![]() ,
, ![]() ,
,
![]() ,设二面角
,设二面角![]() 的平面角为
的平面角为![]() ,
,
则![]()

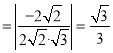 ,
,
由图可知,二面角![]() 的平面角为钝角,
的平面角为钝角,
![]() ,即:二面角
,即:二面角![]() 的余弦值为
的余弦值为![]()


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知集合A={x|x2﹣3x﹣4≤0},B={x|x2﹣2mx+m2﹣9≤0},C={y|y=2x+b,x∈R}
(1)若A∩B=[0,4],求实数m的值;
(2)若A∩C=,求实数b的取值范围;
(3)若A∪B=B,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若二次函数f(x)=x2+bx+c满足f(2)=f(﹣2),且函数的f(x)的一个零点为1. (Ⅰ)求函数f(x)的解析式;
(Ⅱ)对任意的 ![]() ,4m2f(x)+f(x﹣1)≥4﹣4m2恒成立,求实数m的取值范围.
,4m2f(x)+f(x﹣1)≥4﹣4m2恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业为了对生产的一种新产品进行合理定价,将该产品按事先拟定的价格进行试销,得到以下数据:
单价x(元/件) | 60 | 62 | 64 | 66 | 68 | 70 |
销量y(件) | 91 | 84 | 81 | 75 | 70 | 67 |
(I)画出散点图,并求![]() 关于
关于![]() 的回归方程;
的回归方程;
(II)已知该产品的成本是36元/件,预计在今后的销售中,销量与单价仍然服从(I)中的关系,为使企业获得最大利润,该产品的单价应定为多少元(精确到元)?
附:回归直线![]() 的斜率和截距的最小二乘法估计公式分别为:
的斜率和截距的最小二乘法估计公式分别为:
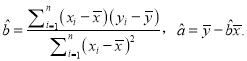
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某单位的职工食堂中,食堂每天以![]() 元/个的价格从面包店购进面包,然后以
元/个的价格从面包店购进面包,然后以![]() 元/个的价格出售.如果当天卖不完,剩下的面包以
元/个的价格出售.如果当天卖不完,剩下的面包以![]() 元/个的价格卖给饲料加工厂.根据以往统计资料,得到食堂每天面包需求量的频率分布直方图如下图所示.食堂某天购进了90个面包,以
元/个的价格卖给饲料加工厂.根据以往统计资料,得到食堂每天面包需求量的频率分布直方图如下图所示.食堂某天购进了90个面包,以![]() (单位:个,
(单位:个, ![]() )表示面包的需求量,
)表示面包的需求量, ![]() (单位:元)表示利润.
(单位:元)表示利润.

(Ⅰ)求![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(Ⅱ)根据直方图估计利润![]() 不少于
不少于![]() 元的概率;
元的概率;
(III)在直方图的需求量分组中,以各组的区间中点值代表该组的各个值,并以需求量落入该区间的频率作为需求量取该区间中间值的概率(例如:若需求量![]() ,则取
,则取![]() ,且
,且![]() 的概率等于需求量落入
的概率等于需求量落入![]() 的频率),求
的频率),求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x+ ![]() (Ⅰ)判断函数的奇偶性,并加以证明;
(Ⅰ)判断函数的奇偶性,并加以证明;
(Ⅱ)用定义证明f(x)在(0,1)上是减函数;
(Ⅲ)函数f(x)在(﹣1,0)上是单调增函数还是单调减函数?(直接写出答案,不要求写证明过程).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次国际学术会议上,来自四个国家的五位代表被安排坐在一张圆桌,为了使他们能够自由交谈,事先了解到的情况如下:
甲是中国人,还会说英语.
乙是法国人,还会说日语.
丙是英国人,还会说法语.
丁是日本人,还会说汉语.
戊是法国人,还会说德语.
则这五位代表的座位顺序应为( )
A. 甲丙丁戊乙 B. 甲丁丙乙戊
C. 甲乙丙丁戊 D. 甲丙戊乙丁
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com