某公司今年年初支出100万元购买一种新的设备,而且公司每年需要支出设备的维修费和工人工资等各种费用,第一年4万元,第二年6万元,以后每年均比上一年增加2万元.除去各种费用后,预计公司每年纯收益为28万元.问:
(1)引进这种设备后,从第几年起该公司开始获利?(即:总收益大于各种支出)
(2)这种设备使用多少年,该公司的年平均收益最大?
解:(1)由题意知,每年的费用是以4为首项,2为公差的等差数列,
设纯收益与使用年数n的关系为f(n),
则f(n)=28n-[4n+
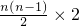
]-100
=25n-n
2-100.…(4分)
由f(n)>0,得n
2-25n+100<0,
解得:5<n<20,
又∵n∈N,所以6,7,8,…,19.
且当n=5时,f(n)=0,
即第5年末的收益与支出恰好相等,故从第6年起该公司开始获利.…(6分)
(2)年平均收益为:
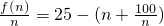
≤25-2

=5.…(10分)
当且仅当n=
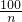
,即n=10时,
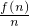
取得最大值.
即这种设备使用10年,该公司的年平均收益最大.…(12分)
分析:(1)由题意知,每年的费用是以4为首项,2为公差的等差数列,设纯收益与使用年数n的关系为f(n),f(n)=28n-[4n+
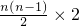
]-100,由此能够求出引进这种设备后,第5年末的收益与支出恰好相等,故从第6年起该公司开始获利.
(2)年平均收益为
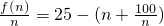
≤25-2×10=5.由此能够求出这种设备使用10年,该公司的年平均收益最大.
点评:本题考查数列在生产实际中的综合应用,考查运算求解能力,推理论证能力;考查函数与方程思想,化归与转化思想.综合性强,难度大,是高考的重点.解题时要认真审题,仔细解答,注意均值定理的灵活运用.

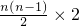 ]-100
]-100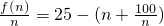
 =5.…(10分)
=5.…(10分)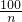 ,即n=10时,
,即n=10时,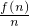 取得最大值.
取得最大值.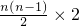 ]-100,由此能够求出引进这种设备后,第5年末的收益与支出恰好相等,故从第6年起该公司开始获利.
]-100,由此能够求出引进这种设备后,第5年末的收益与支出恰好相等,故从第6年起该公司开始获利.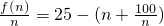 ≤25-2×10=5.由此能够求出这种设备使用10年,该公司的年平均收益最大.
≤25-2×10=5.由此能够求出这种设备使用10年,该公司的年平均收益最大.
