

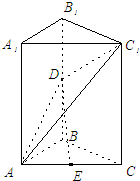
思路解析:E点在AD上变化,EF为平面ADF内变化的一组相交直线(都过定点F),要证明C1F与EF垂直,必有C1F⊥平面ADF.求FC1与平面ABB1A1所成角的关键是找C1到面ABB1A1的垂线,从而落实线面成角,在直三棱柱中,侧棱AA1⊥平面A1B1C1给找点C1到面AB1的垂线创造了方便的条件.
(1)证明:∵AB=AC,且D是BC的中点,∴AD⊥BC.
又∵在直三棱柱中,BB1⊥平面ABC,∴AD⊥BB1.
∴AD⊥平面BB1C1C.∴AD⊥C1F.
在矩形BB1C1C中,BF=BC=2a,B1F=a,
∴DF=![]() a,FC1=
a,FC1=![]() a,DC1=
a,DC1=![]() a.
a.
∴DF2+FC12=DC12.∴∠DFC1=90°,即FC1⊥DF.
∴FC1⊥平面ADF.∴FC1⊥EF.

(2)解:过点C1作C1H⊥A1B1于点H,
∵AA1⊥平面A1B1C1,∴AA1⊥C1H.
∴C1H⊥平面AA1B1B.连结FH,∠C1FH是C1F与平面AB1所成的角.
在等腰△ABC中,AB=AC=3a,BC=2a,∴AD=2![]() a.
a.
在等腰△A1B1C1中,由面积相等,可得C1H×3a=2![]() a×2a,∴C1H=
a×2a,∴C1H=![]() a.又C1F=
a.又C1F=![]() a,
a,
在Rt△C1HF中,sin∠C1FH=![]() ,∴∠C1FH=arcsin
,∴∠C1FH=arcsin![]() ,
,
即C1F与平面AB1所成的角为arcsin![]() .
.


 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:高中数学 来源: 题型:
 如图所示,已知在直三棱柱ABO-A1B1O1中,∠AOB=
如图所示,已知在直三棱柱ABO-A1B1O1中,∠AOB=| π | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图所示,在直三棱柱ABC-A1B1C1中,已知AB=BC=1,∠ABC=90°,AA1=
如图所示,在直三棱柱ABC-A1B1C1中,已知AB=BC=1,∠ABC=90°,AA1=| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知在直三棱柱ABC-A1B1C1中,AB=BB1=2,BC=1,∠ABC=90°,E、F分别为AA1、C1B1的中点,沿棱柱的表面从E到F两点的最短路径的长度为
如图,已知在直三棱柱ABC-A1B1C1中,AB=BB1=2,BC=1,∠ABC=90°,E、F分别为AA1、C1B1的中点,沿棱柱的表面从E到F两点的最短路径的长度为| 5 |
| 2 |
| 5 |
| 2 |
查看答案和解析>>
科目:高中数学 来源:模拟题 题型:解答题
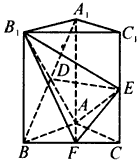
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com