
【题目】设不等式|x﹣2|<a(a∈N*)的解集为A,且 ![]() ∈A,
∈A, ![]() A.
A.
(1)求a的值;
(2)求函数f(x)=|x+a|+|x﹣2|的最小值.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】⊙O1和⊙O2的极坐标方程分别为ρ=4cosθ,ρ=﹣4sinθ.
(1)⊙O1和⊙O2的极坐标方程化为直角坐标方程;
(2)求经过⊙O1和⊙O2交点的直线的直角坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】第二十九届夏季奥林匹克运动会将于2008年8月8日在北京举行,若集合A={参加北京奥运会比赛的运动员},集合B={参加北京奥运会比赛的男运动员}.集合C={参加北京奥运会比赛的女运动员},则下列关系正确的是( )
A.AB
B.BC
C.A∩B=C
D.B∪C=A
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛掷一枚质地均匀的硬币,正面朝上的概率为![]() .现采用随机模拟试验的方法估计抛掷这枚硬币三次恰有两次正面朝上的概率:先由计算器产生0或1的随机数,用0表示正面朝上,用1表示反面朝上;再以每三个随机数做为一组,代表这三次投掷的结果.经随机模拟试验产生了如下20组随机数:
.现采用随机模拟试验的方法估计抛掷这枚硬币三次恰有两次正面朝上的概率:先由计算器产生0或1的随机数,用0表示正面朝上,用1表示反面朝上;再以每三个随机数做为一组,代表这三次投掷的结果.经随机模拟试验产生了如下20组随机数:
101 111 010 101 010 100 100 011 111 110
000 011 010 001 111 011 100 000 101 101
据此估计,抛掷这枚硬币三次恰有两次正面朝上的概率为( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某蛋糕店出售一种蛋糕,这种蛋糕的保质期很短,必须当天卖掉,否则容易变质,该蛋糕店每天以每块16元的成本价格制作这种蛋糕若干块,然后以每块26元的价格出售,如果当天卖不完,剩下的蛋糕只能以每块6元低价出售.蛋糕店记录了100天该种蛋糕的日需求量n(单位:块,n∈N*)整理得如图: 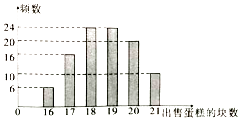
(1)若该蛋糕店某一天制作19块蛋糕,求当天的利润y(单位:元)关于当天需求量n的函数解析式;
(2)若要求出售“出售的蛋糕块数不小于n”的频率不小于0.4,求n的最大值.
(3)若该蛋糕店这100天每天都制作19块蛋糕,试计算这100天蛋糕店所获利润的平均数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com