
【题目】三名工人加工同一种零件,他们在一天中的工作情况如图所示,其中Ai的横、纵坐标分别为第i名工人上午的工作时间和加工的零件数,点Bi的横、纵坐标分别为第i名工人下午的工作时间和加工的零件数,i=1,2,3.
①记Qi为第i名工人在这一天中加工的零件总数,则Q1 , Q2 , Q3中最大的是 .
②记pi为第i名工人在这一天中平均每小时加工的零件数,则p1 , p2 , p3中最大的是 . 
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P﹣ABC中,PA⊥底面ABC,∠BAC=90°.点D,E,N分别为棱PA,PC,BC的中点,M是线段AD的中点,PA=AC=4,AB=2.
(Ⅰ)求证:MN∥平面BDE;
(Ⅱ)求二面角C﹣EM﹣N的正弦值;
(Ⅲ)已知点H在棱PA上,且直线NH与直线BE所成角的余弦值为 ![]() ,求线段AH的长.
,求线段AH的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l、m,平面α、β,下列命题正确的是 ( )
A. l∥β,lαα∥β
B. l∥β,m∥β,lα,mαα∥β
C. l∥m,lα,mβα∥β
D. l∥β,m∥β,lα,mα,l∩m=Mα∥β
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知抛物线x2=y,点A(﹣ ![]() ,
, ![]() ),B(
),B( ![]() ,
, ![]() ),抛物线上的点P(x,y)(﹣
),抛物线上的点P(x,y)(﹣ ![]() <x<
<x< ![]() ),过点B作直线AP的垂线,垂足为Q.
),过点B作直线AP的垂线,垂足为Q.
(Ⅰ)求直线AP斜率的取值范围;
(Ⅱ)求|PA||PQ|的最大值.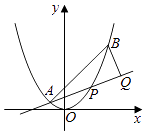
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知空间中三点A(-2,0,2),B(-1,1,2),C(-3,0,4),设a=![]() ,b=
,b=![]() .
.
(1)求向量a与向量b的夹角的余弦值;
(2)若ka+b与ka-2b互相垂直,求实数k的值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=excosx﹣x.(13分)
(1)求曲线y=f(x)在点(0,f(0))处的切线方程;
(2)求函数f(x)在区间[0, ![]() ]上的最大值和最小值.
]上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3+ax2+bx+1(a>0,b∈R)有极值,且导函数f′(x)的极值点是f(x)的零点.(极值点是指函数取极值时对应的自变量的值)
(Ⅰ)求b关于a的函数关系式,并写出定义域;
(Ⅱ)证明:b2>3a;
(Ⅲ)若f(x),f′(x)这两个函数的所有极值之和不小于﹣ ![]() ,求a的取值范围.
,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
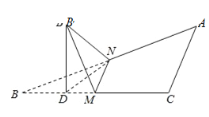
【题目】如图,∠C=![]() ,AC=BC,M、N分别是BC、AB的中点,将△BMN沿直线MN折起,使二面角B′﹣MN﹣B的大小为
,AC=BC,M、N分别是BC、AB的中点,将△BMN沿直线MN折起,使二面角B′﹣MN﹣B的大小为![]() ,则B'N与平面ABC所成角的正切值是( )
,则B'N与平面ABC所成角的正切值是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com