
【题目】已知函数![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)若函数![]() 存在两个极值点
存在两个极值点![]() 且满足
且满足![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)见解析;(2)![]()
【解析】试题分析:(1)求出![]() ,分五种情况讨论
,分五种情况讨论![]() 的范围,分别令
的范围,分别令![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 增区间,
增区间,![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 的减区间;(2)由(1)可知,
的减区间;(2)由(1)可知,![]() ,不等式
,不等式![]() 化为
化为![]() ,令
,令![]() ,则
,则![]() ,
,![]() ,利用导数研究函数的单调性,证明当
,利用导数研究函数的单调性,证明当![]() 时,不等式不成立,当
时,不等式不成立,当![]() 时,可证明
时,可证明![]() ,适量题意,即
,适量题意,即![]() .
.
试题解析:(1)定义域为![]() ,
,
![]() ,
,
当![]() 或
或![]() 时,
时,![]() 恒成立,
恒成立,
当![]() 时,由
时,由![]() 得
得![]() 或
或![]() ,
,
于是结合函数定义域的分析可得:
当![]() 时,函数
时,函数![]() 在定义域
在定义域![]() 上是增函数;
上是增函数;
当![]() 时,函数
时,函数![]() 定义域为
定义域为![]() ,此时有
,此时有![]() ,
,
于是![]() 在
在![]() 上是增函数,在
上是增函数,在![]() 上是减函数,在
上是减函数,在![]() 上是增函数,
上是增函数,
当![]() 时,函数
时,函数![]() 定义域为
定义域为![]() ,
,
于是![]() 在
在![]() 上为减函数,在
上为减函数,在![]() 上为增函数,
上为增函数,
当![]() 时,函数
时,函数![]() 定义域为
定义域为![]() ,此时有
,此时有![]() ,
,
于是![]() 在
在![]() 上是增函数,在
上是增函数,在![]() 上是减函数,在
上是减函数,在![]() 上是减函数,在
上是减函数,在![]() 上是增函数,
上是增函数,
当![]() 时,函数
时,函数![]() 定义域为
定义域为![]() ,
,
于是![]() 在
在![]() 上是增函数,在
上是增函数,在![]() 上是增函数.
上是增函数.
(2)由(1)知![]() 存在两个极值点时,
存在两个极值点时,![]() 的取值范围是
的取值范围是![]() ,
,
由(1)可知,![]() ,
,

![]() ;
;
不等式![]() 化为
化为![]() ,
,
令![]() ,所以
,所以![]() ,
,
令![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,
,![]() ,
,![]() ,所以
,所以![]() ,不合题意;
,不合题意;
当![]() 时,
时,![]() ,
,![]() ,
,
所以![]() 在
在![]() 上是减函数,所以
上是减函数,所以![]() ,适量题意,即
,适量题意,即![]() .
.
综上,若![]() ,此时正数
,此时正数![]() 的取值范围是
的取值范围是![]() .
.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:高中数学 来源: 题型:
【题目】已知离心率为 ![]() 的椭圆
的椭圆 ![]() =1(a>b>0)的一个焦点为F,过F且与x轴垂直的直线与椭圆交于A、B两点,|AB|=
=1(a>b>0)的一个焦点为F,过F且与x轴垂直的直线与椭圆交于A、B两点,|AB|= ![]() .
.
(1)求此椭圆的方程;
(2)已知直线y=kx+2与椭圆交于C、D两点,若以线段CD为直径的圆过点E(﹣1,0),求k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的离心率为
的离心率为![]() ,依次连接椭圆的四个顶点得到的菱形面积为4.
,依次连接椭圆的四个顶点得到的菱形面积为4.
(1)求椭圆的方程;
(2)过点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
, ![]() 两点,设
两点,设![]() 与
与![]() 面积之比为
面积之比为![]() (其中
(其中![]() 为坐标原点),当
为坐标原点),当![]() 时,求实数
时,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() (a>b>0)上一点与它的左、右两个焦点F1 , F2的距离之和为2
(a>b>0)上一点与它的左、右两个焦点F1 , F2的距离之和为2 ![]() ,且它的离心率与双曲线x2﹣y2=2的离心率互为倒数.
,且它的离心率与双曲线x2﹣y2=2的离心率互为倒数.
(1)求椭圆的方程;
(2)如图,点A为椭圆上一动点(非长轴端点),AF1的延长线与椭圆交于点B,AO的延长线与椭圆交于点C.
①当直线AB的斜率存在时,求证:直线AB与BC的斜率之积为定值;
②求△ABC面积的最大值,并求此时直线AB的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知k∈R,直线l1:x+ky=0过定点P,直线l2:kx﹣y﹣2k+2=0过定点Q,两直线交于点M,则|MP|+|MQ|的最大值是( )
A.2 ![]()
B.4
C.4 ![]()
D.8
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在以![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的五面体中,平面
为顶点的五面体中,平面![]() 平面
平面![]() ,
,![]() ,四边形
,四边形![]() 为平行四边形,且
为平行四边形,且![]() .
.
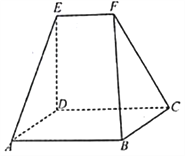
(1)求证:![]() ;
;
(2)若![]() ,
,![]() ,直线
,直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,求平面
,求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】①线性回归方程对应的直线![]() 至少经过其样本数据点
至少经过其样本数据点![]() 中的一个点;
中的一个点;
②若两个变量的线性相关性越强,则相关系数的绝对值越接近于![]() ;
;
③在某项测量中,测量结果![]() 服从正态分布
服从正态分布![]()
![]() ,若
,若![]() 位于区域
位于区域![]() 内的概率为
内的概率为![]() ,则
,则![]() 位于区域
位于区域![]() 内的概率为
内的概率为![]() ;
;
④对分类变量![]() 与
与![]() 的随机变量K2的观测值k来说,k越小,判断“
的随机变量K2的观测值k来说,k越小,判断“![]() 与
与![]() 有关系”的把握越大.其中真命题的序号为( )
有关系”的把握越大.其中真命题的序号为( )
A. ①④ B. ②④ C. ①③ D. ②③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com