
 如图,在棱长为1的正方体ABCD-A1B1C1D1中,点E是棱BC的中点,点F在棱CC1上,且CF=2FC1,P是侧面四边形BCC1B1内一点(含边界),若A1P∥平面AEF,则直线A1P与面BCC1B1所成角的正弦值的取值范围是( )
如图,在棱长为1的正方体ABCD-A1B1C1D1中,点E是棱BC的中点,点F在棱CC1上,且CF=2FC1,P是侧面四边形BCC1B1内一点(含边界),若A1P∥平面AEF,则直线A1P与面BCC1B1所成角的正弦值的取值范围是( )| A. | $[\frac{{2\sqrt{5}}}{5},\frac{{5\sqrt{29}}}{29}]$ | B. | $[\frac{{3\sqrt{13}}}{13},\frac{{5\sqrt{29}}}{29}]$ | C. | $[\frac{{3\sqrt{13}}}{13},\frac{{2\sqrt{2}}}{3}]$ | D. | $[\frac{{2\sqrt{5}}}{5},\frac{{2\sqrt{2}}}{3}]$ |
分析 分别取棱BB1、B1C1的中点M、N,连接MN,易证平面A1MN∥平面AEF,由题意知点P必在线段MN上,由此可判断P在M或N处时A1P最长,位于线段MN中点处时最短,通过解直角三角形即可求得.
解答 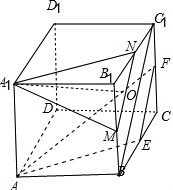 解:如下图所示:
解:如下图所示:
分别取棱BB1、B1C1的中点M、N,连接MN,连接BC1,
∵M、N、E、F为所在棱的中点,∴MN∥BC1,EF∥BC1,
∴MN∥EF,又MN?平面AEF,EF?平面AEF,
∴MN∥平面AEF;
∵AA1∥NE,AA1=NE,∴四边形AENA1为平行四边形,
∴A1N∥AE,又A1N?平面AEF,AE?平面AEF,
∴A1N∥平面AEF,
又A1N∩MN=N,∴平面A1MN∥平面AEF,
∵P是侧面BCC1B1内一点,且A1P∥平面AEF,
则P必在线段MN上,
在Rt△A1B1M中,A1M=$\sqrt{{A}_{1}{{B}_{1}}^{2}+{B}_{1}{M}^{2}}$=$\sqrt{1+(\frac{1}{2})^{2}}$=$\frac{\sqrt{5}}{2}$,
同理,在Rt△A1B1N中,求得A1N=$\frac{\sqrt{5}}{2}$,
∴△A1MN为等腰三角形,
当P在MN中点O时A1P⊥MN,此时A1P最短,P位于M、N处时A1P最长,
A1O=$\sqrt{{A}_{1}{M}^{2}-O{M}^{2}}$=$\sqrt{(\frac{\sqrt{5}}{2})^{2}-(\frac{\sqrt{2}}{4})^{2}}$=$\frac{3\sqrt{2}}{4}$,
A1M=A1N=$\frac{\sqrt{5}}{2}$,
所以线段A1P长度的取值范围是[$\frac{3\sqrt{2}}{4}$,$\frac{\sqrt{5}}{2}$].
直线A1P与面BCC1B1所成角的正弦值的最小值为:$\frac{1}{\frac{\sqrt{5}}{2}}$=$\frac{2\sqrt{5}}{5}$.
直线A1P与面BCC1B1所成角的正弦值最大值为:$\frac{1}{\frac{3\sqrt{2}}{4}}$=$\frac{2\sqrt{2}}{3}$.
直线A1P与面BCC1B1所成角的正弦值的取值范围是:[$\frac{2\sqrt{5}}{5}$,$\frac{2\sqrt{2}}{3}$].
故选:D.
点评 本题考查点、线、面间的距离问题,考查学生的运算能力及推理转化能力,属中档题,解决本题的关键是通过构造平行平面寻找P点位置.


科目:高中数学 来源: 题型:选择题
| A. | ${log_{\frac{1}{3}}}5$ | B. | 5 | C. | -5 | D. | ${({\frac{1}{3}})^5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $16\sqrt{3}$ | B. | $\frac{{16\sqrt{3}}}{3}$ | C. | $9\sqrt{3}$ | D. | $3\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,1) | B. | (1,+∞) | C. | (0,1) | D. | (1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{4}{3}$ | B. | -$\frac{7}{2}$ | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{9}{4}$ | C. | 4 | D. | $\frac{9}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com