
【题目】如图,长方体ABCD﹣A1B1C1D1中,AB=BC=4,BB1=2![]() ,点E、F、M分别为C1D1,A1D1,B1C1的中点,过点M的平面α与平面DEF平行,且与长方体的面相交,交线围成一个几何图形.
,点E、F、M分别为C1D1,A1D1,B1C1的中点,过点M的平面α与平面DEF平行,且与长方体的面相交,交线围成一个几何图形.
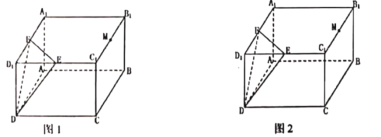
(1)在图1中,画出这个几何图形,并求这个几何图形的面积(不必说明画法与理由)
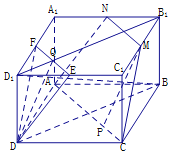
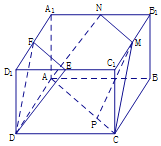
(2)在图2中,求证:D1B⊥平面DEF.
【答案】(1)6![]() (2)见解析
(2)见解析
【解析】
(1)取A1 B1中点为N,连接N与M,则几何图形为ACMN,再求其面积。
(2)建系,利用向量的数量积等于0,说明两直线垂直。
(1)设N为A1B1的中点,连结MN,AN、AC、CM,
则四边形MNAC为所作图形.
由题意知MN∥A1C1(或∥EF),四边形MNAC为梯形,
且MN![]() AC=2
AC=2![]() ,
,
过M作MP⊥AC于点P,
可得MC![]() 2
2![]() ,PC
,PC![]() ,
,
得MP![]() ,
,
∴梯形MNAC的面积![]() (2
(2![]() 4
4![]() )
)![]() 6
6![]() .
.
证明:(2)示例一:在长方体中ABCD﹣A1B1C1D1,
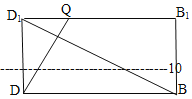
设D1B1交EF于Q,连接DQ,
则Q为EF的中点并且为D1B1的四等点,如图,
D1Q![]() 4
4![]() ,
,
由DE=DF得DQ⊥EF,又EF⊥BB1,
∴EF⊥平面BB1D1D,∴EF⊥D1B,
![]() ,∴∠D1QD=∠BD1D,
,∴∠D1QD=∠BD1D,
∴∠QD1B+∠D1QD=∠DD1B+∠BD1Q=90°,
∴DQ⊥D1B,∴D1B⊥平面DEF.
示例二:设D1B1交EF于Q,连接DQ,则Q为EF的中点,
且为D1B1的四等分点,D1Q![]() 4
4![]() ,
,
由BB1⊥平面A1B1C1D1可知BB1⊥EF,
又B1D1⊥EF,BB1∩B1D1=B1,∴EF⊥平面BB1D1D,∴EF⊥D1B,
由![]() ,得tan∠QDD1=tan∠D1BD,
,得tan∠QDD1=tan∠D1BD,
得∠QDD1=∠D1BD,∴∠QDB+∠D1BD=∠QDB+∠QDD1=90°,
∴DQ⊥D1B,又DQ∩EF=Q,∴D1B⊥平面DEF.
 ;
;


科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系中,以原点为极点,以![]() 轴的非负半轴为极轴且取相同的单位长度建立极坐标系,曲线
轴的非负半轴为极轴且取相同的单位长度建立极坐标系,曲线![]() 的极坐标方程为:
的极坐标方程为:![]() .
.
(1)若曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),求曲线
为参数),求曲线![]() 的直角坐标方程和曲线
的直角坐标方程和曲线![]() 的普通方程;
的普通方程;
(2)若曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),
为参数),![]() ,且曲线
,且曲线![]() 与曲线
与曲线![]() 的交点分别为
的交点分别为![]() 、
、![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国际上钻石的重量计算单位为克拉.已知某种钻石的价值y(美元)与其重量x(克拉)的平方成正比,且一颗为3克拉的该种钻石的价值为54000美元.已知,价值损失百分率![]() 切割中重量的损耗不计.
切割中重量的损耗不计.
(1)写出y关于x的函数关系式;
(2)若把一颗钻石切割成重量比为![]() 的两颗钻石,求价值损失的百分率;
的两颗钻石,求价值损失的百分率;
(3)若把一颗钻石切割成重量分别为m克拉和n克拉的两颗钻石,问:当m、n满足何种关系时,价值损失的百分率最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a>0,a≠1,设p:函数y=loga(x+3)在(0,+∞)上单调递减,q:函数y=x2+(2a-3)x+1的图像与x轴交于不同的两点.如果p∨q真,p∧q假,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com