
【题目】设函数![]() ,
,![]() ,其中
,其中![]() ,
,![]()
![]() .
.
(1)求![]() 的单调区间;
的单调区间;
(2)若![]() 存在极值点
存在极值点![]() ,且
,且![]() ,其中
,其中![]() ,求证:
,求证:![]() ;
;
(3)设![]() ,函数
,函数![]() ,求证:
,求证:![]() 在区间
在区间![]() 上的最大值不小于
上的最大值不小于![]() .
.
【答案】(1)当![]() 时,
时,![]() 的单调递增区间为
的单调递增区间为![]() ,
,![]() ,单调递减区间为
,单调递减区间为![]() ,单调递增区间为
,单调递增区间为![]() ,
,![]() ;(2)证明见解析;(3)证明见解析.
;(2)证明见解析;(3)证明见解析.
【解析】
试题分析:(1)求出![]() 的导数,讨论
的导数,讨论![]() 时,
时,![]() ,
,![]() 在
在![]() 上递增;当
上递增;当![]() 时,由导数大
时,由导数大
于![]() ,可得增区间;导数小于
,可得增区间;导数小于![]() ,可得减区间;(2)
,可得减区间;(2)![]() ,可得
,可得![]() ,分别计算
,分别计算![]() ,
,![]() ,化简整理即可得证;(3)要证
,化简整理即可得证;(3)要证![]() 在区间
在区间![]() 上的最大值不小于
上的最大值不小于![]() ,即证在
,即证在![]() 上存在
上存在![]() ,
,![]() ,使得
,使得![]() ,运用单调性和极值,化简整理即可得证.
,运用单调性和极值,化简整理即可得证.
试题解析:(1)解:由![]() ,可得
,可得![]() .
.
下面分两种情况讨论:
①当![]() 时,有
时,有![]() 恒成立,所以
恒成立,所以![]() 的单调递增区间为
的单调递增区间为![]() ;
;
②当![]() 时,令
时,令![]() ,解得
,解得![]() ,或
,或![]() .
.
当![]() 变化时,
变化时,![]() ,
,![]() 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
|
| 0 |
| 0 |
|
|
| 极大值 |
| 极小值 |
|
所以![]() 的单调递减区间为
的单调递减区间为![]() ,单调递增区间为
,单调递增区间为![]() ,
,![]() .
.
(2)证明:因为![]() 存在极值点,所以由(1)知
存在极值点,所以由(1)知![]() ,且
,且![]() ,
,
由题意,得![]() ,即
,即![]() ,
,
进而![]() ,
,
又![]()
![]()
![]() ,
,
即为![]() ,即有
,即有![]() ,即为
,即为![]() .
.
(3)要证![]() 在区间
在区间![]() 上的最大值不小于
上的最大值不小于![]() ,即证在
,即证在![]() 上存在
上存在![]() ,
,![]() ,使得
,使得![]() ,
,
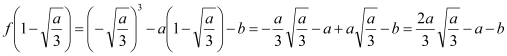 ,
,
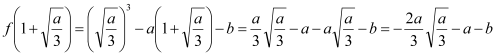 ,
,
![]() ,
,![]() ,
,![]() ,
,
由于![]() ,
,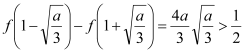 成立.
成立.
综上可得,![]() 在区间
在区间![]() 上的最大值不小于
上的最大值不小于![]() .
.


科目:高中数学 来源: 题型:
【题目】为选拔参加“全市高中数学竞赛”的选手,某中学举行了一次“数学竞赛”活动.为了了解本次竞赛学生的成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为![]() 分)作为样本(样本容量为
分)作为样本(样本容量为![]() )进行统计.按照
)进行统计.按照![]() 的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在
的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在![]() 的数据).
的数据).
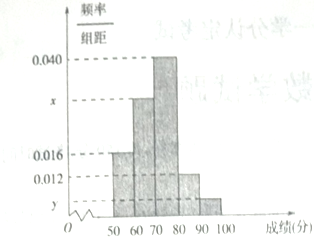
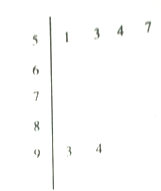
(1)求样本容![]() 和频率分布直方图中
和频率分布直方图中![]() 的值并求出抽取学生的平均分;
的值并求出抽取学生的平均分;
(2)在选取的样本中,从竞赛成绩在![]() 分以上(含
分以上(含![]() 分)的学生中随机抽取
分)的学生中随机抽取![]() 名学生参加“全市中数学竞赛”求所抽取的
名学生参加“全市中数学竞赛”求所抽取的![]() 名学生中至少有一人得分在
名学生中至少有一人得分在![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥PABCD中,底面ABCD是正方形,侧棱PD垂直于底面ABCD,PD=DC,点E是PC的中点.
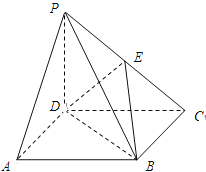
(Ⅰ)求证:PA∥平面EBD;
(Ⅱ)求二面角EBDP的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某科研小组研究发现:一棵水蜜桃树的产量![]() (单位:百千克)与肥料费用
(单位:百千克)与肥料费用![]() (单位:百元)满足如下关系:
(单位:百元)满足如下关系:![]() ,且投入的肥料费用不超过5百元.此外,还需要投入其他成本(如施肥的人工费等)
,且投入的肥料费用不超过5百元.此外,还需要投入其他成本(如施肥的人工费等)![]() 百元.已知这种水蜜桃的市场售价为16元/千克(即16百元/百千克),且市场需求始终供不应求.记该棵水蜜桃树获得的利润为
百元.已知这种水蜜桃的市场售价为16元/千克(即16百元/百千克),且市场需求始终供不应求.记该棵水蜜桃树获得的利润为![]() (单位:百元).
(单位:百元).
(1)求利润函数![]() 的函数关系式,并写出定义域;
的函数关系式,并写出定义域;
(2)当投入的肥料费用为多少时,该水蜜桃树获得的利润最大?最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】先后2次抛掷一枚骰子,将得到的点数分别记为![]() .
.
(Ⅰ)求满足![]() 的概率;
的概率;
(Ⅱ)设三条线段的长分别为![]() 和5,求这三条线段能围成等腰三角形(含等边三角形)的概率.
和5,求这三条线段能围成等腰三角形(含等边三角形)的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的极坐标方程为
的极坐标方程为![]() ,
, ![]() 与
与![]() 的交点为
的交点为![]() .
.
(1)判断点![]() 与曲线
与曲线![]() 的位置关系;
的位置关系;
(2)点![]() 为曲线
为曲线![]() 上的任意一点,求
上的任意一点,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《中国好声音(The Voice of China)》是由浙江卫视联合星空传媒旗下灿星制作强力打造的大型励志专业音乐评论节目,于2012年7月13日正式在浙江卫视播出.每期节目有四位导师参加.导师背对歌手,当每位参赛选手演唱完之前有导师为其转身,则该选手可以选择加入为其转身的导师的团队中接受指导训练.已知某期《中国好声音》中,6位选手演唱完后,四位导师为其转身的情况如下表所示:

现从这6位选手中随机抽取两人考查他们演唱完后导师的转身情况.
(1)求选出的两人导师为其转身的人数和为4的概率;
(2)记选出的2人导师为其转身的人数之和为![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com