
分析 运用分段函数求得m+n=1,再由乘1法和基本不等式,即可得到所求最小值.
解答 解:函数f(x)=$\left\{\begin{array}{l}{lo{g}_{3}(x+2),x≥1}\\{{e}^{x}-1,x<1}\end{array}\right.$,
m+n=f[f(ln2)]=f(eln2-1)=f(2-1)=log33=1,
则$\frac{1}{m}+\frac{2}{n}$=(m+n)($\frac{1}{m}+\frac{2}{n}$)=3+$\frac{n}{m}$+$\frac{2m}{n}$≥3+2$\sqrt{\frac{n}{m}•\frac{2m}{n}}$=3+2$\sqrt{2}$,
当且仅当n=$\sqrt{2}$m时,取得最小值3+2$\sqrt{2}$.
故答案为:3+2$\sqrt{2}$.
点评 本题考查基本不等式的运用:求最值,注意运用乘1法,考查分段函数值的计算,属于中档题.


科目:高中数学 来源: 题型:解答题
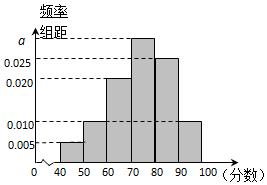 某校从高二年级学生中随机抽取40名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100]后得到如图的频率分布直方图.
某校从高二年级学生中随机抽取40名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100]后得到如图的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
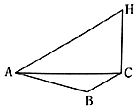 为了应对日益严重的气候问题,某气象仪器科研单位研究出一种新的“弹射型”气候仪器,这种仪器可以弹射到空中进行气候观测,如图所示,A,B,C三地位于同一水平面上,这种仪器在C地进行弹射实验,观测点A,B两地相距100米,∠BAC=60°,在A地听到弹射声音比B地晚$\frac{2}{17}$秒(已知声音传播速度为340米/秒),在A地测得该仪器至高点H处的仰角为30°,则这种仪器的垂直弹射高度HC=140$\sqrt{3}$米.
为了应对日益严重的气候问题,某气象仪器科研单位研究出一种新的“弹射型”气候仪器,这种仪器可以弹射到空中进行气候观测,如图所示,A,B,C三地位于同一水平面上,这种仪器在C地进行弹射实验,观测点A,B两地相距100米,∠BAC=60°,在A地听到弹射声音比B地晚$\frac{2}{17}$秒(已知声音传播速度为340米/秒),在A地测得该仪器至高点H处的仰角为30°,则这种仪器的垂直弹射高度HC=140$\sqrt{3}$米.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 气温(°C) | 20 | 16 | 12 | 4 |
| 用电量(度) | 14 | 28 | 44 | 62 |
| A. | 70 | B. | 68 | C. | 64 | D. | 62 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com