
【题目】在如图所示的多面体![]() 中,底面四边形
中,底面四边形![]() 是菱形,
是菱形,![]() ,
,![]() ,
,![]() 相交于
相交于![]() ,
,![]() ,
,![]() 在平面
在平面![]() 上的射影恰好是线段
上的射影恰好是线段![]() 的中点
的中点![]() .
.
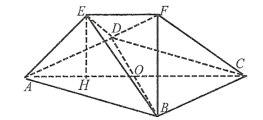
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)若直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,求平面
,求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
【答案】(Ⅰ)见解析;(Ⅱ)![]() .
.
【解析】试题分析:(1)证明线面垂直先证明线线垂直,EH⊥BD,AC⊥BD,∴BD⊥平面EACF,即BD⊥平面ACF;(2)建立空间坐标系,求两个平面的法向量,根据向量夹角的求法得到面面角.
解析:
(Ⅰ)取AO的中点H,连结EH,则EH⊥平面ABCD
∵BD在平面ABCD内,∴EH⊥BD
又菱形ABCD中,AC⊥BD 且EH∩AC=H,EH、AC在平面EACF内
∴BD⊥平面EACF,即BD⊥平面ACF
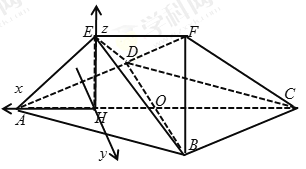
(Ⅱ)由(Ⅰ)知EH⊥平面ABCD,以H为原点,如图所示建立空间直角坐标系H﹣xyz
∵EH⊥平面ABCD,∴∠EAH为AE与平面ABCD所成的角,
即∠EAH=45°,又菱形ABCD的边长为4,则![]()
各点坐标分别为![]() ,
,
E(0,0,![]() )
)
易知![]() 为平面ABCD的一个法向量,记
为平面ABCD的一个法向量,记![]() =
=![]() ,
,![]() =
=![]() ,
,![]() =
=![]()
∵EF∥AC,∴![]() =
=![]()
设平面DEF的一个法向量为![]() (注意:此处
(注意:此处![]() 可以用
可以用![]() 替代)
替代)
即 ![]() =
=![]() ,
,![]()
令![]() ,则,∴
,则,∴![]()
∴![]()
平面DEF与平面ABCD所成角(锐角)的余弦值为![]() .
.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源: 题型:
【题目】2017年8月20日起,市交警支队全面启动路口秩序环境综合治理,重点整治机动车不礼让斑马线和行人的行为,经过一段时间的治理,从市交警队数据库中调取了20个路口近三个月的车辆违章数据,经统计得如图所示的频率分布直方图,统计数据中凡违章车次超过30次的设为“重点关注路口”.
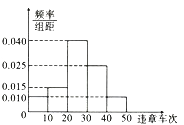
(1)现从“重点关注路口”中随机抽取两个路口安排交警去执勤,求抽出来的路口的违章车次一个在![]() ,一个在
,一个在![]() 中的概率;
中的概率;
(2)现从支队派遣5位交警,每人选择一个路口执勤,每个路口至多1人,违章车次在![]() 的路口必须有交警去,违章车次在
的路口必须有交警去,违章车次在![]() 的不需要交警过去,设去“重点关注路口”的交警人数为
的不需要交警过去,设去“重点关注路口”的交警人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知曲线![]() 在平面直角坐标系
在平面直角坐标系![]() 下的参数方程为
下的参数方程为 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系.
轴正半轴为极轴,建立极坐标系.
(1)求曲线![]() 的普通方程及极坐标方程;
的普通方程及极坐标方程;
(2)直线![]() 的极坐标方程是
的极坐标方程是![]() ,射线
,射线![]() :
: ![]() 与曲线
与曲线![]() 交于点
交于点![]() 与直线
与直线![]() 交于点
交于点![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 若f(x1)=f(x2),且x1<x2,关于下列命题:(1)f(x1)>f(﹣x2);(2)f(x2)>f(﹣x1);(3)f(x1)>f(﹣x1);(4)f(x2)>f(﹣x2).正确的个数为( )
若f(x1)=f(x2),且x1<x2,关于下列命题:(1)f(x1)>f(﹣x2);(2)f(x2)>f(﹣x1);(3)f(x1)>f(﹣x1);(4)f(x2)>f(﹣x2).正确的个数为( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com