
【题目】已知函数![]() 在
在![]() 处有极值
处有极值![]() .
.
(Ⅰ)求实数![]() 的值;
的值;
(Ⅱ)设![]() ,讨论函数
,讨论函数![]() 在区间
在区间![]() 上的单调性.
上的单调性.
【答案】(1) ![]() 在
在![]() 处有极值
处有极值![]() 时,
时,![]() ,(2)见解析.
,(2)见解析.
【解析】试题分析:(Ⅰ)求出导函数,由∴![]() 且
且![]() ,求得
,求得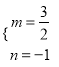 或
或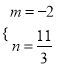 ,检验后可得结果;(Ⅱ)由(Ⅰ)可知
,检验后可得结果;(Ⅱ)由(Ⅰ)可知![]() ,利用导数研究函数的单调性和极值,分五种情况讨论,分别比较极值与端点处的函数值即可得结果.
,利用导数研究函数的单调性和极值,分五种情况讨论,分别比较极值与端点处的函数值即可得结果.
试题解析:(Ⅰ)![]() 定义域为
定义域为![]() ,
,
∵![]() 在
在![]() 处有极值
处有极值![]() ,
,
∴![]() 且
且![]() ,
,
即![]()
解得:![]() 或
或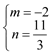
当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]()
∴![]() 在
在![]() 处有极值
处有极值![]() 时,
时,![]() .
.
(Ⅱ)由(Ⅰ)可知![]() ,其单调性和极值分布情况如表:
,其单调性和极值分布情况如表:
|
|
|
|
|
|
| + | 0 | - | 0 | + |
| 增 | 极大 | 减 | 极小 | 增 |
∴①当![]() ,即
,即![]() 时,
时,![]() 在区间
在区间![]() 上的单调递增;
上的单调递增;
②当![]() ,即
,即![]() 时,
时,![]() 在区间
在区间![]() 上单调递增,在区间
上单调递增,在区间![]() 上单调递减;③当
上单调递减;③当![]() 且
且![]() ,即
,即![]() 时,
时,![]() 在区间
在区间![]() 上单调递减;
上单调递减;
④当![]() ,即
,即![]() 时,
时,![]() 在区间
在区间![]() 上的单调递减,在区间
上的单调递减,在区间![]() 上单调递增;
上单调递增;
⑤![]() 时,
时,![]() 在区间
在区间![]() 上单调递增.
上单调递增.
综上所述,当![]() 时函数
时函数![]() 在区间
在区间![]() 上的单调性为:
上的单调性为:
![]() 或
或![]() 时,单调递增;
时,单调递增;
![]() 时,在
时,在![]() 上的单调递增,在
上的单调递增,在![]() 上单调递减;
上单调递减;
![]() 时,单调递减;
时,单调递减;
![]() 时,在
时,在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
【方法点晴】本题主要考查的是利用导数研究函数的单调性、利用导数研究函数的极值与最值,属于难题.利用导数研究函数![]() 的单调性进一步求函数最值的步骤:①确定函数
的单调性进一步求函数最值的步骤:①确定函数![]() 的定义域;②对
的定义域;②对![]() 求导;③令
求导;③令![]() ,解不等式得
,解不等式得![]() 的范围就是递增区间;令
的范围就是递增区间;令![]() ,解不等式得
,解不等式得![]() 的范围就是递减区间;④根据单调性求函数
的范围就是递减区间;④根据单调性求函数![]() 的极值及最值(闭区间上还要注意比较端点处函数值的大小).
的极值及最值(闭区间上还要注意比较端点处函数值的大小).


科目:高中数学 来源: 题型:
【题目】平面上两点A(﹣1,0),B(1,0),在圆C:(x﹣3)2+(y﹣4)2=4上取一点P,
(Ⅰ)x﹣y+c≥0恒成立,求c的范围
(Ⅱ)从x+y+1=0上的点向圆引切线,求切线长的最小值
(Ⅲ)求|PA|2+|PB|2的最值及此时点P的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班学生进行了三次数学测试,第一次有8名学生得满分,第二次有10名学生得满分,第三次有12名学生得满分,已知前两次均为满分的学生有5名,三次测试中至少又一次得满分的学生有15名.若后两次均为满分的学生至多有![]() 名,则
名,则![]() 的值为( )
的值为( )
A. 7 B. 8 C. 9 D. 10
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知O为坐标原点,F是椭圆C: ![]() =1(a>b>0)的左焦点,A,B分别为C的左,右顶点.P为C上一点,且PF⊥x轴,过点A的直线l与线段PF交于点M,与y轴交于点E.若直线BM经过OE的中点,则C的离心率为( )
=1(a>b>0)的左焦点,A,B分别为C的左,右顶点.P为C上一点,且PF⊥x轴,过点A的直线l与线段PF交于点M,与y轴交于点E.若直线BM经过OE的中点,则C的离心率为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个袋中装有四个形状大小完全相同的球,球的编号分别为1,2,3,4.
(Ⅰ)从袋中随机抽取两个球,求取出的球的编号之和不大于4的概率;
(Ⅱ)先从袋中随机取一个球,该球的编号为m,将球放回袋中,然后再从袋中随机取一个球,该球的编号为n,求n<m+2的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某车间20名工人年龄数据如下表:
年龄(岁) | 工人数(人) |
19 | 1 |
28 | 3 |
29 | 3 |
30 | 5 |
31 | 4 |
32 | 3 |
40 | 1 |
合计 | 20 |
(1)求这20名工人年龄的众数与极差;
(2)以十位数为茎,个位数为叶,作出这20名工人年龄的茎叶图;
(3)求这20名工人年龄的方差.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 是奇函数。
是奇函数。
(1)求实数m的值;
(2)判断函数f(x)在(1,+∞)上的单调性,并给出证明;
(3)当x∈(n,a-2)时,函数f(x)的值域是(1,+∞),求实数a与n的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】稳定房价是我国今年实施宏观调控的重点,国家最近出台的一系列政策已对各地的房地产市场产生了影响.北京市某房地产介绍所对本市一楼群在今年的房价作了统计与预测:发现每个季度的平均单价y(每平方米面积的价格,单位为元)与第x季度之间近似满足:y=500sin(ωx+)+9500 (>0),已知第一、二季度平均单价如下表所示:
x | 1 | 2 | 3 |
y | 10000 | 9500 | ? |
则此楼群在第三季度的平均单价大约是 ( )
A.10000元
B.9500元
C.9000元
D.8500元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=log2(x+1),g(x)=log2(3x+1).
(1)求出使g(x)≥f(x)成立的x的取值范围;
(2)当x∈[0,+∞)时,求函数y=g(x)﹣f(x)的值域.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com