
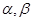 为平面,且m
为平面,且m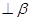 ,则“m//
,则“m//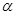 ”是“
”是“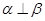 ”的充要条件;
”的充要条件;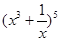 的展开式中含x3的项的系数为60;
的展开式中含x3的项的系数为60;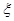 ~N(0,1),若P(
~N(0,1),若P(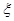 ≥2)=p,则P(-2<
≥2)=p,则P(-2<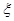 <0)=
<0)=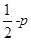 ;
;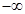 ,2);
,2);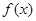 满足
满足 ,且0<x<
,且0<x<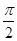 时
时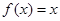 ,则函数
,则函数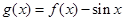 在[
在[ ,
,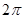 ]上有5个零点.
]上有5个零点. ,所以,由
,所以,由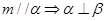 成立,
成立,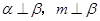 ,可得到
,可得到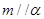 或
或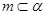 ,所以
,所以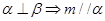 不成立,故该命题为假命題;
不成立,故该命题为假命題;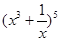 的展开式中第
的展开式中第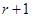 项
项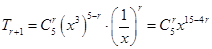 ,
,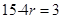 ,解得
,解得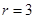 ,所以有
,所以有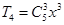 =
=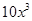 ,
,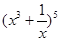 的展开式中含x3的项的系数为10而不是60;故该命题是假命题.
的展开式中含x3的项的系数为10而不是60;故该命题是假命题.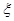 ~N(0,1),若P(
~N(0,1),若P(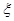 ≥2)=p,则
≥2)=p,则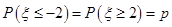 ,
,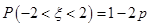
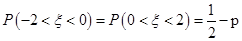 ;该命题是真命题;
;该命题是真命题;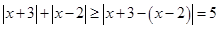
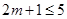 ,解得
,解得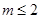
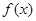 满足
满足 ,所以,
,所以,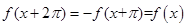 ,故函数
,故函数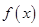 是周期函数,且
是周期函数,且 ;同样由奇函数
;同样由奇函数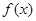 满足
满足 ,
,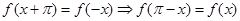
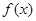 的图象关于直线
的图象关于直线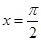 对称;
对称;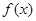 满足当0<x<
满足当0<x<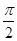 时
时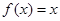 得当
得当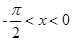 时,
时, 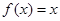 ,
,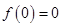
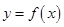 和
和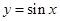 的图象如下图,则两图象在区间
的图象如下图,则两图象在区间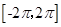 内交点的个数就是函数
内交点的个数就是函数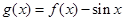 在区间
在区间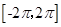 内的零点的个数;但由于
内的零点的个数;但由于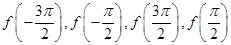 的值不能确定,故零点的个数不能确定,
的值不能确定,故零点的个数不能确定,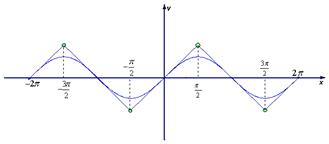


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:高中数学 来源:不详 题型:解答题
 中, 四边形
中, 四边形 是正方形,
是正方形, ,
, .将正方形沿
.将正方形沿 折起,得到如图2所示的多面体,其中面
折起,得到如图2所示的多面体,其中面 面
面 ,
, 是
是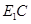 中点.
中点. ∥平面
∥平面 ;
; 的体积.
的体积.

查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 AB.Q是PC上的一点.
AB.Q是PC上的一点.
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
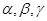 是三个不重合的平面,
是三个不重合的平面, 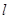 是直线,给出下列四个命题:①若
是直线,给出下列四个命题:①若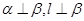 则
则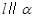 ;②若
;②若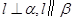 则
则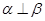 ;③若
;③若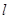 上有两点到
上有两点到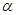 的距离相等,则
的距离相等,则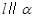 ;④若
;④若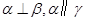 ,则
,则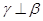 其中正确命题的序号 ( )
其中正确命题的序号 ( )| A.②④ | B.①④ | C.②③ | D.①② |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com