
【题目】海上某货轮在A处看灯塔B在货轮的北偏东75°,距离为12![]() 海里;在A处看灯塔C在货轮的北偏西30°,距离为8
海里;在A处看灯塔C在货轮的北偏西30°,距离为8![]() 海里;货轮向正北由A处行驶到D处时看灯塔B在货轮的北偏东120°.(要画图)
海里;货轮向正北由A处行驶到D处时看灯塔B在货轮的北偏东120°.(要画图)
(1)A处与D处之间的距离;
(2)灯塔C与D处之间的距离.
 名师指导一卷通系列答案
名师指导一卷通系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=log2(x+1),g(x)=log2(3x+1).
(1)求出使g(x)≥f(x)成立的x的取值范围;
(2)在(1)的范围内求y=g(x)﹣f(x)的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知海岛A到海岸公路BC的距离AB=50km,B,C间的距离为100km,从A到C必须先坐船到BC上的某一点D,航速为25km/h,再乘汽车到C,车速为50km/h,记∠BDA=θ
(1)试将由A到C所用的时间t表示为θ的函数t(θ);
(2)问θ为多少时,由A到C所用的时间t最少?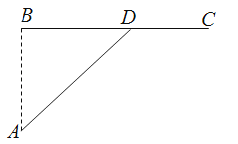
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为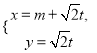 (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点, ![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,且直线
,且直线![]() 经过曲线
经过曲线![]() 的左焦点
的左焦点![]() .
.
(1)求直线![]() 的普通方程;
的普通方程;
(2)设曲线![]() 的内接矩形的周长为
的内接矩形的周长为![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物,我国PM2.5标准采用世卫组织设定的最宽限值,即PM2.5日均值在35微克/立方米以下空气质量为一级;在35微克/立方米~75微克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标.某市环保局从市区2017年上半年每天的PM2.5监测数据中随机抽取15天的数据作为样本,监测值如茎叶图所示(十位为茎,个位为叶)
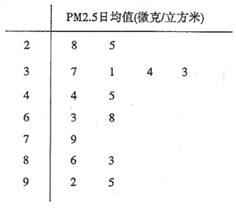
(1)从这15天的数据中任取一天,求这天空气质量达到一级的概率;
(2)从这15天的数据中任取3天的数据,记![]() 表示其中空气质量达到一级的天数,求
表示其中空气质量达到一级的天数,求![]() 的分布列;
的分布列;
(3)以这15天的PM2.5的日均值来估计一年的空气质量情况,(一年按360天来计算),则一年中大约有多少天的空气质量达到一级.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com