
【题目】某年级![]() 位同学参加语文和数学两门课的考试,每门课的考分从0到100分. 假如考试的结果没有两位同学的成绩是完全相同的(即至少有一门课的成绩不同). 另外,“甲比乙好”是指同学甲的语文和数学的考分均分别高于同学乙的语文和数学的考分. 试问:当
位同学参加语文和数学两门课的考试,每门课的考分从0到100分. 假如考试的结果没有两位同学的成绩是完全相同的(即至少有一门课的成绩不同). 另外,“甲比乙好”是指同学甲的语文和数学的考分均分别高于同学乙的语文和数学的考分. 试问:当![]() 最小为何值时,必存在三位同学(设为甲、乙、丙),有甲比乙好,乙比丙好.
最小为何值时,必存在三位同学(设为甲、乙、丙),有甲比乙好,乙比丙好.
 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:
【题目】有10名选手![]() ,他们的积分分别为9,8,7,6,5,4,3,2,1,0,名次分别为第1,2,3,4,5,6,7,8,9,10.现进行单循环比赛(即任意两名选手之间都恰进行一场比赛),且每场比赛都要分出胜负.若名次靠前的选手胜了名次靠后的选手,则胜者得1分,负者得0分;若名次靠后的选手胜了名次靠前的选手,则胜者得2分,负者得0分.全部比赛结束后计算每名选手的累计积分(即这次单循环所得的分数与之前的积分相加所得的和),并根据累计积分进行重新排名,求新的冠军累计积分的最小值(允许名次并列).
,他们的积分分别为9,8,7,6,5,4,3,2,1,0,名次分别为第1,2,3,4,5,6,7,8,9,10.现进行单循环比赛(即任意两名选手之间都恰进行一场比赛),且每场比赛都要分出胜负.若名次靠前的选手胜了名次靠后的选手,则胜者得1分,负者得0分;若名次靠后的选手胜了名次靠前的选手,则胜者得2分,负者得0分.全部比赛结束后计算每名选手的累计积分(即这次单循环所得的分数与之前的积分相加所得的和),并根据累计积分进行重新排名,求新的冠军累计积分的最小值(允许名次并列).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个盒子里装有大小均匀的![]() 个小球,其中有红色球
个小球,其中有红色球![]() 个,编号分别为
个,编号分别为![]() ;白色球
;白色球![]() 个, 编号分别为
个, 编号分别为![]() , 从盒子中任取
, 从盒子中任取![]() 个小球(假设取到任何—个小球的可能性相同).
个小球(假设取到任何—个小球的可能性相同).
(1)求取出的![]() 个小球中,含有编号为
个小球中,含有编号为![]() 的小球的概率;
的小球的概率;
(2)在取出的![]() 个小球中, 小球编号的最大值设为
个小球中, 小球编号的最大值设为![]() ,求随机变量
,求随机变量![]() 的分布列.
的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 若命题![]() 均为真命题,则命题
均为真命题,则命题![]() 为真命题
为真命题
B. “若![]() ,则
,则![]() ”的否命题是“若
”的否命题是“若![]() ”
”
C. 在![]() ,“
,“![]() ”是“
”是“![]() ”的充要条件
”的充要条件
D. 命题![]() “
“![]() ”的否定为
”的否定为![]() “
“![]() ”
”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某学校准备修建一个面积为2400平方米的矩形活动场地(图中ABCD)的围栏,按照修建要求,中间用围墙EF隔开,使得ABEF为矩形,EFCD为正方形,设![]() 米,已知围墙(包括EF)的修建费用均为每米500元,设围墙(包括EF)的修建总费用为y元.
米,已知围墙(包括EF)的修建费用均为每米500元,设围墙(包括EF)的修建总费用为y元.
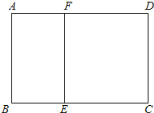
(1)求出y关于x的函数解析式及x的取值范围;
(2)当x为何值时,围墙(包括EF)的修建总费用y最小?并求出y的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】自出生之日起,人的情绪、体力、智力等心理、生理状况就呈周期变化,变化由线为![]() .根据心理学家的统计,人体节律分为体力节律、情绪节律和智力节律三种.这些节律的时间周期分别为23天、28天、33天.每个节律周期又分为高潮期、临界日和低潮期三个阶段.以上三个节律周期的半数为临界日,这就是说11.5天、14天、16.5天分别为体力节律、情绪节律和智力节律的临界日.临界日的前半期为高潮期,后半期为低潮期.生日前一天是起始位置(平衡位置),已知小英的生日是2003年3月20日(每年按365天计算).
.根据心理学家的统计,人体节律分为体力节律、情绪节律和智力节律三种.这些节律的时间周期分别为23天、28天、33天.每个节律周期又分为高潮期、临界日和低潮期三个阶段.以上三个节律周期的半数为临界日,这就是说11.5天、14天、16.5天分别为体力节律、情绪节律和智力节律的临界日.临界日的前半期为高潮期,后半期为低潮期.生日前一天是起始位置(平衡位置),已知小英的生日是2003年3月20日(每年按365天计算).
(1)请写出小英的体力、情绪和智力节律曲线的函数;
(2)试判断小英在2019年4月22日三种节律各处于什么阶段,当日小英是否适合参加某项体育竞技比赛?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 点为圆
点为圆![]() 上的动点,点
上的动点,点![]() 在
在![]() 轴上的投影为
轴上的投影为![]() ,动点
,动点![]() 满足
满足![]() ,动点
,动点![]() 的轨迹为
的轨迹为![]() .
.
(Ⅰ)求![]() 的方程;
的方程;
(Ⅱ)设![]() 的左顶点为
的左顶点为![]() ,若直线
,若直线![]() 与曲线
与曲线![]() 交于两点
交于两点![]() ,
,![]() (
(![]() ,
,![]() 不是左右顶点),且满足
不是左右顶点),且满足![]() ,求证:直线
,求证:直线![]() 恒过定点,并求出该定点的坐标.
恒过定点,并求出该定点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com