
【题目】已知函数f(x)=( ![]() )x , 函数g(x)=log
)x , 函数g(x)=log ![]() x.
x.
(1)若g(ax2+2x+1)的定义域为R,求实数a的取值范围;
(2)当x∈[( ![]() )t+1 , (
)t+1 , ( ![]() )t]时,求函数y=[g(x)]2﹣2g(x)+2的最小值h(t);
)t]时,求函数y=[g(x)]2﹣2g(x)+2的最小值h(t);
(3)是否存在非负实数m,n,使得函数y=log ![]() f(x2)的定义域为[m,n],值域为[2m,2n],若存在,求出m,n的值;若不存在,则说明理由.
f(x2)的定义域为[m,n],值域为[2m,2n],若存在,求出m,n的值;若不存在,则说明理由.
【答案】
(1)解: ![]() 定义域为R;
定义域为R;
所以ax2+2x+1>0对一切x∈R成立;
当a=0时,2x+1>0不可能对一切x∈R成立;
所以 ![]() 即:
即: ![]() ;
;
综上 a>1
(2)解: ![]() ;
;
令 ![]() ;
;
所以y=u2﹣2u+2=(u﹣1)2+1,u∈[t,t+1];
当t≥1时, ![]() ;
;
当0<t<1时,ymin=1;
当t≤0时, ![]() ;
;
所以 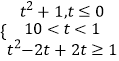
(3)解:y=x2在[0,+∞)上是增函数;
若存在非负实数m、n满足题意,则 ![]() ;
;
即m、n是方程x2=2x的两非负实根,且m<n;
所以m=0,n=2;
即存在m=0,n=2满足题意
【解析】(1)g(ax2+2x+1)的定义域为R,即所以ax2+2x+1>0对一切x∈R成立,转化为一元二次函数问题;(2)利用换元法构造新函数y=u2﹣2u+2=(u﹣1)2+1,u∈[t,t+1];对参数t分类讨论其位置,判断函数的最小值即可;(3)根据函数的单调性,列出方程组 ![]() ,转化为:即m、n是方程x2=2x的两非负实根,且m<n;
,转化为:即m、n是方程x2=2x的两非负实根,且m<n;


 一线名师提优试卷系列答案
一线名师提优试卷系列答案科目:高中数学 来源: 题型:
【题目】已知命题p:方程x2+mx+1=0有两个不等的负实数根;命题q:方程4x2+4(m﹣2)x+1=0无实数根.
(1)若“¬p”为假命题,求m范围;
(2)若“p或q”为真命题,“p且q”为假命题,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若{ ![]() 、
、 ![]() 、
、 ![]() }为空间的一组基底,则下列各项中,能构成基底的一组向量是( )
}为空间的一组基底,则下列各项中,能构成基底的一组向量是( )
A.![]() ,
, ![]() +
+ ![]() ,
, ![]() ﹣
﹣ ![]()
B.![]() ,
, ![]() +
+ ![]() ,
, ![]() ﹣
﹣ ![]()
C.![]() ,
, ![]() +
+ ![]() ,
, ![]() ﹣
﹣ ![]()
D.![]() +
+ ![]() ,
, ![]() ﹣
﹣ ![]() ,
, ![]() +2
+2 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数g(x)=f(x)+2x,x∈R为奇函数.
(1)判断函数f(x)的奇偶性;
(2)若x>0时,f(x)=log3x,求函数g(x)的解析式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,AB=1,AC=2,BC= ![]() ,D,E分别是AC1和BB1的中点,则直线DE与平面BB1C1C所成的角为( )
,D,E分别是AC1和BB1的中点,则直线DE与平面BB1C1C所成的角为( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某上市股票在30天内每股的交易价格P(元)与时间t(天)组成有序数对(t,P),点(t,P)落在下图中的两条线段上,该股票在30天内(包括30天)的日交易量Q(万股)与时间t(天)的部分数据如下表所示. 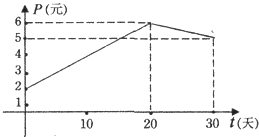
第t天 | 4 | 10 | 16 | 22 |
Q(万股) | 36 | 30 | 24 | 18 |
(1)根据提供的图象,写出该种股票每股交易价格P(元)与时间t(天)所满足的函数关系式;
(2)根据表中数据确定日交易量Q(万股)与时间t(天)的一次函数关系式;
(3)在(2)的结论下,用y(万元)表示该股票日交易额,写出y关于t的函数关系式,并求出这30天中第几日交易额最大,最大值为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:x2=4y的焦点为F,过点F且斜率为1的直线与抛物线相交于M、N两点,设直线l是抛物线C的切线,且l∥MN,P为l上一点,则 ![]() 的最小值为 .
的最小值为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com