
分析 f′(x)=3ax2+2x+b,由于x=1时f(x)有极小值-2,可得f′(1)=0,f(1)=-2,解得a,b.不等式f′(x)+4>n(xlnx-1),即:x2+2x+1>n(xlnx-1),(x>0).令x0lnx0=1.则x0∈(1,2),当x>x0时,xlnx-1>0,又x2+2x+1>0.因此只考虑x>x0时,n的最大值即可.$n<\frac{{x}^{2}+2x+1}{xlnx-1}$=g(x),
x>x0.利用导数研究其单调性极值与最值即可.
解答 解:f′(x)=3ax2+2x+b,
∵x=1时f(x)有极小值-2,
∴f′(1)=3a+2+b=0,f(1)=a+1+b-$\frac{1}{3}$=-2,
解得$a=\frac{1}{3}$,b=-3.
∴f′(x)=x2+2x-3=(x+3)(x-1),满足条件.
不等式f′(x)+4>n(xlnx-1),
即:x2+2x+1>n(xlnx-1),(x>0).
令x0lnx0=1.则x0∈(1,2),当x>x0时,xlnx-1>0,
又x2+2x+1>0.
因此只考虑x>x0时,n的最大值即可.
$n<\frac{{x}^{2}+2x+1}{xlnx-1}$=g(x),x>x0.
g′(x)=$\frac{(2x+2)(xlnx-1)-({x}^{2}+2x+1)(lnx+1)}{(xlnx-1)^{2}}$=$\frac{(x+1)[(x-1)lnx-(x+3)]}{(xlnx-1)^{2}}$.
令h(x)=(x-1)lnx-(x+3),
h′(x)=lnx-$\frac{1}{x}$>0,
∴h(x)在(x0,+∞)上单调递增,
∴h(x)>h(x0)=(x0-1)lnx0-(x0+3)=-$\frac{1}{{x}_{0}}$-x0-2.
h(6)=5ln6-9=5×1.791-9<0.
h(7)=6ln7-10>0.
∴h(x)的零点x1∈(6,7).
g(6)=$\frac{49}{6ln6-1}$≈5.03,g(7)=$\frac{64}{7ln7-1}$≈5.07.
∴n<5.03.
∴正整数n的最大值为5.
故答案为:5.
点评 本题考查了利用导数研究其单调性极值与最值、恒成立问题的等价转化方法,考查了推理能力与计算能力,属于难题.


科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{1}{3}$) | B. | ($\frac{1}{3}$,$\frac{2}{3}$) | C. | ($\frac{2}{3}$,1) | D. | (1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
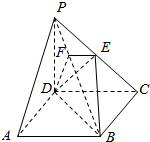 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC=1,点E是PC的中点,作EF⊥PB交PB于点F.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC=1,点E是PC的中点,作EF⊥PB交PB于点F.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com