
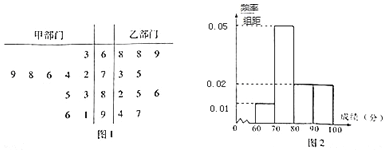
分析 (Ⅰ)利用频率分布直方图能求出甲组数据的中位数.
(Ⅱ)从甲、乙两组数据中各任取一个,基本事件总数n=10×10=100,利用列举法求出所取两数之差的绝对值大于20包含的基本事件的个数,所取两数之差的绝对值大于20的概率.
解答 解:(Ⅰ)设甲组数据中位数为a
则0.01×10+0.05×(a-70)=0.5,解得a=78.
答:估算甲组数据的中位数为78 (4分)
(Ⅱ)从甲、乙两组数据中各任取一个,基本事件总数n=10×10=100,(6分)
所取两数之差的绝对值大于20包含的基本事件有:
(63,85),(63,86),(63,94),(63,97),(72,94),(72,97),
(74,97),(76,97),(68,91),(68,91),(68,96),(68,96),
(69,91),(69,96),(73,96),(75,96),共16个,
∴所取两数之差的绝对值大于20的概率p=$\frac{16}{100}$.(12分)
点评 本题考查茎叶图、频率分布直方图的应用,考查概率的求法,是基础题,解题时要认真审题,注意列举法的合理运用.


科目:高中数学 来源:2015-2016学年江西省南昌市高二文下学期期末考试数学试卷(解析版) 题型:填空题
已知命题 函数
函数 在定义域上单调递增;命题
在定义域上单调递增;命题 不等式
不等式 对任意实数
对任意实数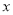 恒成立.若
恒成立.若 是真命题,则实数
是真命题,则实数 的取值范围为_____________.
的取值范围为_____________.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 航空测量组的飞机航线和山顶在同一铅直平面内,已知飞机的高度为海拔10千米,速度为180千米/小时.飞机先看到山顶的俯角为15°,经过420秒后又看到山顶的俯角为45°,求山顶的海拔高度(取$\sqrt{2}=1.4$,$\sqrt{3}=1.7$).
航空测量组的飞机航线和山顶在同一铅直平面内,已知飞机的高度为海拔10千米,速度为180千米/小时.飞机先看到山顶的俯角为15°,经过420秒后又看到山顶的俯角为45°,求山顶的海拔高度(取$\sqrt{2}=1.4$,$\sqrt{3}=1.7$).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com