
【题目】已知函数![]() (
(![]() 且
且![]() 为常数).
为常数).
(1)当![]() 时,讨论函数
时,讨论函数![]() 在
在![]() 的单调性;
的单调性;
(2)设![]() 可求导数,且它的导函数
可求导数,且它的导函数![]() 仍可求导数,则
仍可求导数,则![]() 再次求导所得函数称为原函数
再次求导所得函数称为原函数![]() 的二阶函数,记为
的二阶函数,记为![]() ,利用二阶导函数可以判断一个函数的凹凸性.一个二阶可导的函数在区间
,利用二阶导函数可以判断一个函数的凹凸性.一个二阶可导的函数在区间![]() 上是凸函数的充要条件是这个函数在
上是凸函数的充要条件是这个函数在![]() 的二阶导函数非负.
的二阶导函数非负.
若![]() 在
在![]() 不是凸函数,求
不是凸函数,求![]() 的取值范围.
的取值范围.
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:高中数学 来源: 题型:
【题目】(本小题满分12分)
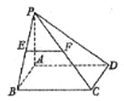
如图,在四棱锥P—ABCD中,底面ABCD是矩形,PA⊥平面ABCD,AP=AB,BP=BC=2,E,F分别是PB,PC的中点.
(Ⅰ)证明:EF∥平面PAD;
(Ⅱ)求三棱锥E—ABC的体积V.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业准备投入适当的广告费对甲产品进行促销宣传,在一年内预计销量![]() (万件)与广告费
(万件)与广告费![]() (万元)之间的函数关系为
(万元)之间的函数关系为![]() ,已知生产此产品的年固定投入为
,已知生产此产品的年固定投入为![]() 万元,每生产1万件此产品仍需要再投入30万元,且能全部销售完,若每件甲产品销售价格(元)定为:“平均每件甲产品生产成本的150%”与“年平均每件产品所占广告费的50%”之和,则当广告费为1万元时,该企业甲产品的年利润比不投入广告费时的年利润增加了__________万元.
万元,每生产1万件此产品仍需要再投入30万元,且能全部销售完,若每件甲产品销售价格(元)定为:“平均每件甲产品生产成本的150%”与“年平均每件产品所占广告费的50%”之和,则当广告费为1万元时,该企业甲产品的年利润比不投入广告费时的年利润增加了__________万元.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一般地,对于直线![]() 及直线
及直线![]() 外一点
外一点![]() ,我们有点
,我们有点![]() 到直线
到直线![]() 的距离公式为:
的距离公式为:![]() ”
”
(1)证明上述点![]() 到直线
到直线![]() 的距离公式
的距离公式
(2)设直线![]() ,试用上述公式求坐标原点
,试用上述公式求坐标原点![]() 到直线
到直线![]() 距离的最大值及取最大值时
距离的最大值及取最大值时![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)的定义域为D,若存在非零实数l使得对于任意x∈M(MD),有x+l∈D,且f(x+l)![]() f(x),则称f(x)为M上的l高调函数.现给出下列命题:①函数f(x)=2﹣x为R上的1高调函数;②函数f(x)=sin2x为R上的π高调函数;③如果定义域为[﹣1,+∞)的函数f(x)=x2为[﹣1,+∞)上m高调函数,那么实数m的取值范围是[2,+∞);④函数f(x)=lg(|x﹣2|+1)为[1,+∞)上的2高调函数.其中真命题的个数为( )
f(x),则称f(x)为M上的l高调函数.现给出下列命题:①函数f(x)=2﹣x为R上的1高调函数;②函数f(x)=sin2x为R上的π高调函数;③如果定义域为[﹣1,+∞)的函数f(x)=x2为[﹣1,+∞)上m高调函数,那么实数m的取值范围是[2,+∞);④函数f(x)=lg(|x﹣2|+1)为[1,+∞)上的2高调函数.其中真命题的个数为( )
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中正确的是( )
A. “![]() ”是“
”是“![]() ”成立的充分不必要条件
”成立的充分不必要条件
B. 命题![]() ,则
,则![]()
C. 为了了解800名学生对学校某项教改试验的意见,用系统抽样的方法从中抽取一个容量为40的样本,则分组的组距为40
D. 已知回归直线的斜率的估计值为1.23,样本点的中心为![]() ,则回归直线方程为
,则回归直线方程为![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com