
【题目】已知复数z=(a2﹣7a+6)+(a2﹣5a﹣6)i(a∈R)
(1)若复数z为纯虚数,求实数a的值;
(2)若复数z在复平面内的对应点在第四象限,求实数a的取值范围.
科目:高中数学 来源: 题型:
【题目】已知a>0,a≠1,设p:函数y=loga(x+1)在(0,+∞)上单调递减;q:曲线y=x2+(2a﹣3)x+1与x轴交于不同的两点.如果p且q为假命题,p或q为真命题,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从参加考试的学生中抽出60名学生,将其成绩(均为整数)分成六组[40,50),[50,60)…[90,100]后,画出如下部分频率分布直方图.观察图形的信息,回答下列问题: (Ⅰ) 求成绩落在[70,80)上的频率,并补全这个频率分布直方图;
(Ⅱ) 估计这次考试的及格率(60分及以上为及格)和平均分;
(Ⅲ) 设学生甲、乙的成绩属于区间[40,50),现从成绩属于该区间的学生中任选两人,求甲、乙中至少有一人被选的概率.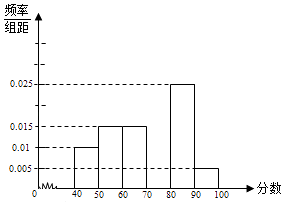
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,某抛物线的顶点为原点
,某抛物线的顶点为原点![]() ,焦点为圆心
,焦点为圆心![]() ,经过点
,经过点![]() 的直线
的直线![]() 交圆
交圆![]() 于
于![]() ,
, ![]() 两点,交此抛物线于
两点,交此抛物线于![]() ,
, ![]() 两点,其中
两点,其中![]() ,
, ![]() 在第一象限,
在第一象限, ![]() ,
, ![]() 在第二象限.
在第二象限.
(1)求该抛物线的方程;
(2)是否存在直线![]() ,使
,使![]() 是
是![]() 与
与![]() 的等差中项?若存在,求直线
的等差中项?若存在,求直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)= ![]() (其中p2+q2≠0),且存在公差不为0的无穷等差数列{an},使得函数在其定义域内还可以表示为f(x)=1+a1x+a2x+a2x2+…+anxn+…
(其中p2+q2≠0),且存在公差不为0的无穷等差数列{an},使得函数在其定义域内还可以表示为f(x)=1+a1x+a2x+a2x2+…+anxn+…
(1)求a1 , a2的值(用p,q表示);
(2)求{an}的通项公式;
(3)当n∈N*且n≥2时,比较(an﹣1)an与(an) ![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
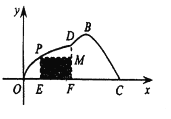
【题目】如图所示,某小区为美化环境,准备在小区内草坪的一侧修建一条直路![]() ,另一侧修建一条休闲大道,它的前一段
,另一侧修建一条休闲大道,它的前一段![]() 是函数
是函数![]() ,
, ![]() 的一部分,后一段
的一部分,后一段![]() 是函数
是函数![]() (
(![]() ,
, ![]() ),
),![]() 时的图象,图象的最高点为
时的图象,图象的最高点为![]() ,
, ![]() ,垂足为
,垂足为![]() .
.
(1)求函数![]() 的解析式;
的解析式;
(2)若在草坪内修建如图所示的儿童游乐园PMFE,问点![]() 落在曲线
落在曲线![]() 上何处时,儿童乐园的面积最大?
上何处时,儿童乐园的面积最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某校5个学生的数学和物理成绩如表
学生的编号i | 1 | 2 | 3 | 4 | 5 |
数学xi | 80 | 75 | 70 | 65 | 60 |
物理yi | 70 | 66 | 68 | 64 | 62 |
(Ⅰ)假设在对这5名学生成绩进行统计时,把这5名学生的物理成绩搞乱了,数学成绩没出现问题,问:恰有2名学生的物理成绩是自己的实际分数的概率是多少?
(Ⅱ)通过大量事实证明发现,一个学生的数学成绩和物理成绩具有很强的线性相关关系的,在上述表格是正确的前提下,用x表示数学成绩,用y表示物理成绩,求y与x的回归方程;
参考公式: ![]() =
= 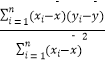 ,
, ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com