
 =(3,1),
=(3,1), =(-1,a),a∈R
=(-1,a),a∈R =(m,2),求a、m的值;
=(m,2),求a、m的值; =
= (
( +
+ )=(1,
)=(1,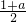 )(2分)
)(2分) =(m,2),∴
=(m,2),∴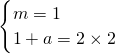 ,解得
,解得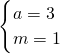 .(7分)
.(7分) •
• =0,则3×(-1)+1•a=0,解得a=3(9分)
=0,则3×(-1)+1•a=0,解得a=3(9分) =
= -
- =(-4,a-1)(10分)
=(-4,a-1)(10分) •
• =0,则-1×(-4)+a•(a-1)=0,解得a无解,
=0,则-1×(-4)+a•(a-1)=0,解得a无解, 的坐标,由题意和向量相等的条件列出方程,求出a和m的值;
的坐标,由题意和向量相等的条件列出方程,求出a和m的值;

 口算题天天练系列答案
口算题天天练系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com