
【题目】如图所示,四棱锥![]() 中,四边形
中,四边形![]() 是直角梯形,
是直角梯形, ![]() 底面
底面![]() ,
, ![]() 为
为![]() 的中点,
的中点, ![]() 点在
点在![]() 上,且
上,且![]() .
.

(1)证明: ![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(I)见解析;(II)![]() ,
,
【解析】试题分析:(1)要证MN∥平面PAD,只需在面PAD内找到一条直线和MN平行即可,而根据条件,易作辅助线过M作ME∥CD交PD于E,连接AE,下证MN∥AE;
(2)求直线MN与平面PCB所成的角,关键找直线MN在平面PCB内的射影,而根据条件,易作辅助线过N点作NQ∥AP交BP于点Q,NF⊥CB交CB于点F,连接QF,过N点作NH⊥QF交QF于H,连接MH,下证NH⊥平面PBC,∴∠NMH为直线MN与平面PCB所成的角.解△MNH即可.
试题解析:
(1)过点![]() 作
作![]() 交
交![]() 于
于![]() 点,连结
点,连结![]() ,
,
![]() , 又
, 又![]()
![]() 为平行四边形,
为平行四边形, ![]() 平面
平面![]() .
.
(2)过![]() 点作
点作![]() 交
交![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,
,
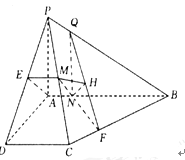
连结![]() ,过
,过![]() 点作
点作![]() 于
于![]() ,连结
,连结![]()
易知![]() 面
面![]() 而
而![]() 面
面![]() ,
,![]()
而![]() 面
面![]() ,
, ![]() 为直线
为直线![]() 与平面
与平面![]() 所成角,
所成角,
![]() 通过计算可得
通过计算可得![]() ,
,
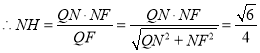 ,
,
![]() ,
,
![]() 直线
直线![]() 与平面
与平面![]() 所成角为
所成角为![]() .
.


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案科目:高中数学 来源: 题型:
【题目】如图已知![]() 是边长为
是边长为![]() 的正方形
的正方形![]() 的中心,点
的中心,点![]() 分别是
分别是![]() 的中点,沿对角线
的中点,沿对角线![]() 把正方形
把正方形![]() 折成二面角
折成二面角![]() .
.

(1)证明:四面体![]() 的外接球的体积为定值,并求出定值;
的外接球的体积为定值,并求出定值;
(2)若二面角![]() 为直二面角,求二面角
为直二面角,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 和
和![]() 满足:
满足:![]() ,
,![]()
![]() ,
,![]() ,其中
,其中![]() .
.
(1)求数列![]() 和
和![]() 的通项公式;
的通项公式;
(2)记数列![]() 的前
的前![]() 项和为
项和为![]() ,问是否存在正整数
,问是否存在正整数![]() ,使得
,使得![]() 成立?若存在,求
成立?若存在,求![]() 的最小值;若不存在,请说明理由.
的最小值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某游乐场推出了一项趣味活动,参加活动者需转动如图所示的转盘两次,每次转动后,待转盘停止转动时,记录指针所指区域中的数.设两次记录的数分别为![]() ,奖励规则如下:①若
,奖励规则如下:①若![]() ,则奖励玩具一个;②若
,则奖励玩具一个;②若![]() ,则奖励水杯一个;③其余情况奖励饮料一瓶.假设转盘质地均匀,四个区域划分均匀,小亮准备参加此项活动.
,则奖励水杯一个;③其余情况奖励饮料一瓶.假设转盘质地均匀,四个区域划分均匀,小亮准备参加此项活动.

(1)求小亮获得玩具的概率;
(2)请比较小亮获得水杯与获得饮料的概率的大小,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学名著《续古摘奇算法》(杨辉)一书中有关于三阶幻方的问题:将1,2,3,4,5,6,7,8,9分别填入![]() 的方格中,使得每一行,每一列及对角线上的三个数的和都相等,我们规定:只要两个幻方的对应位置(如每行第一列的方格)中的数字不全相同,就称为不同的幻方,那么所有不同的三阶幻方的个数是( )
的方格中,使得每一行,每一列及对角线上的三个数的和都相等,我们规定:只要两个幻方的对应位置(如每行第一列的方格)中的数字不全相同,就称为不同的幻方,那么所有不同的三阶幻方的个数是( )
8 | 3 | 4 |
1 | 5 | 9 |
6 | 7 | 2 |
A. 9 B. 8 C. 6 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市为了解各校《国学》课程的教学效果,组织全市各学校高二年级全体学生参加了国学知识水平测试,测试成绩从高到低依次分为A、B、C、D四个等级.随机调阅了甲、乙两所学校各60名学生的成绩,得到如下的分布图:

(Ⅰ)试确定图中![]() 与
与![]() 的值;
的值;
(Ⅱ)若将等级A、B、C、D依次按照![]() 分、80分、60分、50分转换成分数,试分别估计两校学生国学成绩的均值;
分、80分、60分、50分转换成分数,试分别估计两校学生国学成绩的均值;
(Ⅲ)从两校获得A等级的同学中按比例抽取5人参加集训,集训后由于成绩相当,决定从中随机选2人代表本市参加省级比赛,求两人来自同一学校的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂为了对新研发的一种产品进行合理定价,将该定价按事先拟定的价格进行试销,得到如下数据:
单价 | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
销量 | 90 | 84 | 83 | 80 | 75 | 68 |
(1)求回归直线方程![]() ;
;
(2)预计在今后的销售中,销量与单价仍然服从(1)中的关系,且该产品的成本是4元/件,为使工厂获得最大利润,该产品的单价应定为多少元?
附:  .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,过左焦点
,过左焦点![]() 且垂直于长轴的弦长为
且垂直于长轴的弦长为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)点![]() 为椭圆
为椭圆![]() 的长轴上的一个动点,过点
的长轴上的一个动点,过点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,证明:
两点,证明:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业实行裁员增效,已知现有员工![]() 人,每人每年可创纯收益(已扣工资等)1万元,据评估,在生产条件不变的情况下,每裁员一人,则留岗员工每人每年可多创收0.01万元,但每年需付给下岗工人每位0.4万元的生活费,并且企业正常运转所需人数不得少于现有员工的
人,每人每年可创纯收益(已扣工资等)1万元,据评估,在生产条件不变的情况下,每裁员一人,则留岗员工每人每年可多创收0.01万元,但每年需付给下岗工人每位0.4万元的生活费,并且企业正常运转所需人数不得少于现有员工的![]() ,设该企业裁员
,设该企业裁员![]() 人后,年纯收益为
人后,年纯收益为![]() 万元.
万元.
(1)写出![]() 关于
关于![]() 的函数关系式,并指出
的函数关系式,并指出![]() 的取值范围;
的取值范围;
(2)当![]() 时,该企业应裁员多少人,才能获得最大的经济效益(注:在保证能取得最大的经济效益的情况下,能少裁员,应尽量少裁员)?
时,该企业应裁员多少人,才能获得最大的经济效益(注:在保证能取得最大的经济效益的情况下,能少裁员,应尽量少裁员)?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com