
【题目】已知向量 ![]() =(m,cos2x),
=(m,cos2x), ![]() =(sin2x,n),设函数f(x)=
=(sin2x,n),设函数f(x)= ![]()
![]() ,且y=f(x)的图象过点(
,且y=f(x)的图象过点( ![]() ,
, ![]() )和点(
)和点( ![]() ,﹣2).
,﹣2).
(1)求m,n的值;
(2)将y=f(x)的图象向左平移φ(0<φ<π)个单位后得到函数y=g(x)的图象.若y=g(x)的图象上各最高点到点(0,3)的距离的最小值为1,求y=g(x)的单调增区间.
【答案】
(1)解:已知: ![]() ,
, ![]() ,
,
则: ![]() =msin2x+ncos2x,
=msin2x+ncos2x,
y=f(x)的图象过点y=f(x)的图象过点( ![]() ,
, ![]() )和点(
)和点( ![]() ,﹣2).
,﹣2).
则: 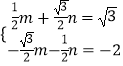 解得:
解得: ![]() ,
,
即:m= ![]() ,n=1
,n=1
故答案为: m= ![]() ,n=1
,n=1
(2)解:由(1)得: ![]() =
= ![]() ,f(x)向左平移φ个单位得到:
,f(x)向左平移φ个单位得到:
g(x)=2sin(2x+2Φ+ ![]() ),
),
设g(x)的对称轴x=x0,最高点的坐标为:(x0,2)点(0,3)的距离的最小值为1,则: ![]() ,
,
则:g(0)=2,
解得:Φ= ![]() ,
,
所以:g(x)=2sin(2x+ ![]() )=2cos2x.
)=2cos2x.
令:﹣π+2kπ≤2x≤2kπ (k∈Z)
则:单调递增区间为:[ ![]() ](k∈Z)
](k∈Z)
故答案为:单调递增区间为:[ ![]() ](k∈Z)
](k∈Z)
【解析】(1)首先根据向量的数量积的坐标运算求得f(x)=msin2x+ncos2x,进一步根据图象经过的点求得:m和n的值.(2)由(1)得: ![]() =
= ![]() ,f(x)向左平移φ个单位得到g(x)=2sin(2x+2Φ+
,f(x)向左平移φ个单位得到g(x)=2sin(2x+2Φ+ ![]() )设g(x)的对称轴x=x0 , 最高点的坐标为:(x0 , 2)点(0,3)的距离的最小值为1,则:g(x)=2sin(2x+
)设g(x)的对称轴x=x0 , 最高点的坐标为:(x0 , 2)点(0,3)的距离的最小值为1,则:g(x)=2sin(2x+ ![]() )=2cos2x,进一步求得单调区间.
)=2cos2x,进一步求得单调区间.
【考点精析】根据题目的已知条件,利用函数y=Asin(ωx+φ)的图象变换的相关知识可以得到问题的答案,需要掌握图象上所有点向左(右)平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的横坐标伸长(缩短)到原来的
的图象上所有点的横坐标伸长(缩短)到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的纵坐标伸长(缩短)到原来的
的图象上所有点的纵坐标伸长(缩短)到原来的![]() 倍(横坐标不变),得到函数
倍(横坐标不变),得到函数![]() 的图象.
的图象.


 口算题天天练系列答案
口算题天天练系列答案科目:高中数学 来源: 题型:
【题目】设Sn是数列{an}的前n项和,已知a1=3,an+1=2Sn+3(n∈N)
(I)求数列{an}的通项公式;
(Ⅱ)令bn=(2n﹣1)an , 求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂甲、乙、丙三个车间生产了同一种产品,数量分别为120件,80件,60件.为了解它们的产品质量是否存在显著差异,用分层抽样方法抽取了一个容量为n的样本进行调查,其中从丙车间的产品中抽取了3件,则n=( )
A.9
B.10
C.12
D.13
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数y=f(x)是定义域为R的偶函数,且在(0,+∞)上单调递减,则( )
A.f(﹣π)>f(﹣1)>f( ![]() )
)
B.f(﹣1)>f(﹣π)>f( ![]() )
)
C.f(﹣π)>f( ![]() )>f(﹣1)
)>f(﹣1)
D.f(﹣1)>f( ![]() )>f(﹣π)
)>f(﹣π)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,一个矩形花园里需要铺两条笔直的小路,已知矩形花园长AD=5m,宽AB=3m,其中一条小路定为AC,另一条小路过点D,问如何在BC上找到一点M,使得两条小路AC与DM相互垂直?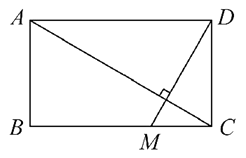
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com