
分析 当直线l斜率存在时,设直线方程为y=kx+b,联立方程由韦达定理可得x1+x2=$\frac{-2kb}{1+{k}^{2}}$,x1x2=$\frac{{b}^{2}-1}{1+{k}^{2}}$,由三角形的面积可得∠POQ=90°,进而可得$\overrightarrow{OP}$•$\overrightarrow{OQ}$=0,可得2b2=k2-1,代入x12+x22=(x1+x2)2-2x1x2,化简可得.
解答 解:当直线l斜率存在时,设直线方程为y=kx+b,
和圆的方程联立消y并整理得(1+k2)x2+2kbx+b2-1=0,
由韦达定理可得x1+x2=$\frac{-2kb}{1+{k}^{2}}$,x1x2=$\frac{{b}^{2}-1}{1+{k}^{2}}$,
∵△OPQ的面积为$\frac{1}{2}$,∴$\frac{1}{2}$×1×1×sin∠POQ=$\frac{1}{2}$,
∴sin∠POQ=1,∠POQ=90°,
∴$\overrightarrow{OP}$•$\overrightarrow{OQ}$=x1x2+y1y2=x1x2+(kx1+b)(kx2+b)
=(1+k2)x1x2+kb(x1+x2)+b2
=(1+k2)$\frac{{b}^{2}-1}{1+{k}^{2}}$+kb$\frac{-2kb}{1+{k}^{2}}$+b2=0,
化简可得2b2=k2-1,
∴x12+x22=(x1+x2)2-2x1x2
=$\frac{2{b}^{2}({k}^{2}-1)+2(1+{k}^{2})}{(1+{k}^{2})^{2}}$=1
验证可得当直线斜率不存在时,仍有x12+x22=1
故答案为:1
点评 本题考查直线和圆的位置关系,涉及三角形的面积公式和韦达定理以及向量的垂直,属中档题.


科目:高中数学 来源: 题型:选择题
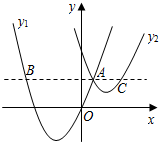 如图,抛物线y1=a(x+2)2-3与y2=$\frac{1}{2}$(x-3)2+1交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.则以下结论:
如图,抛物线y1=a(x+2)2-3与y2=$\frac{1}{2}$(x-3)2+1交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.则以下结论:| A. | ①② | B. | ②③ | C. | ③④ | D. | ①④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 很大的实数可以构成集合 | |
| B. | 自然数集N中最小的数是1 | |
| C. | 集合{y|y=x2-1}与集合{(x,y)|y=x2-1}是同一个集合 | |
| D. | 空集是任何集合的子集. |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 7 | C. | 2$\sqrt{2}$ | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (5,6) | B. | (4,5) | C. | (3,4) | D. | (2,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| φx+φ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| x | $\frac{π}{12}$ | $\frac{7π}{12}$ | $\frac{5π}{6}$ | ||
| Asin(φx+φ) | 0 | 3 | 0 | -3 | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com