练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】某单位安排7位员工对一周的7个夜晚值班，每位员工值一个夜班且不重复值班，其中员工甲必须安排在星期一或星期二值班，员工乙不能安排在星期二值班，员工丙必须安排在星期五值班，则这个单位安排夜晚值班的方案共有（ ）

    A. 96种B. 144种C. 200种D. 216种

    【答案】D

    【解析】

    可分为两类：甲安排在星期一，丙排在星期五和甲安排在星期二，丙排在星期五，再由分类计数原理，即可求解．

    由题意，先安排丙和甲，再安排乙，其余的人任意排．

    若甲安排在星期一，丙排在星期五，则乙有4种安排方法，其余的4人任意排，共有4=96种．

    若甲安排在星期二，丙排在星期五，则其余的5人任意排，共有=120种．

    由分类计数原理，可得这个单位安排夜晚值班的方案共有96+120=216种，

    故选：D．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，在三棱锥中，，，为的中点．

    （1）证明：平面；

    （2）若点在棱上，且，求点到平面的距离．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在三棱锥中，平面平面，为等边三角形，，且，O，M分别为，的中点．

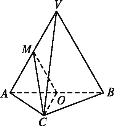
    （Ⅰ）求证：平面；

    （Ⅱ）设是线段上一点，满足平面平面，试说明点的位置；

    （Ⅲ）求三棱锥的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】函数的最大值为3,其图象相邻两条对称轴之间的距离为.

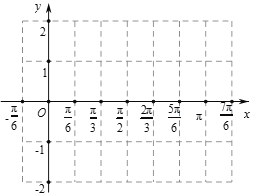
    (Ⅰ)求函数的解析式和当时的单调减区间；

    (Ⅱ)的图象向右平行移动个长度单位,再向下平移1个长度单位,得到的图象,用“五点法”作出在内的大致图象.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】朱世杰是历史上最伟大的数学家之一，他所著的《四元玉鉴》卷中“如像招数”五问中有如下问题：“今有官司差夫一千八百六十四人筑堤，只云初日差六十四人，次日转多七人，每人日支米三升，共支米四百三石九斗二升，问筑堤几日”。其大意为“官府陆续派遣1864人前往修筑堤坝，第一天派出64人，从第二天开始每天派出的人数比前一天多7人，修筑堤坝的每人每天分发大米3升，共发出大米40392升，问修筑堤坝多少天”，在该问题中前5天共分发了多少大米？

    A. 1170升 B. 1380升 C. 3090升 D. 3300升

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的中心在原点，焦点在轴上，短轴长和焦距都等于2， 是椭圆上的一点，且在第一象限内，过且斜率等于的直线与椭圆交于另一点，点关于原点的对称点为.

    （Ⅰ）证明：直线的斜率为定值；

    （Ⅱ）求面积的最大值，并求此时直线的方程.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】给出下列命题：

    (1)终边在y轴上的角的集合是；

    (2)把函数f(x)＝2sin2x的图象沿x轴方向向左平移个单位后，得到的函数解析式可以表示成f(x)＝2sin；

    (3)函数f(x)＝sinx＋的值域是[－1,1]；

    (4)已知函数f(x)＝2cosx，若存在实数x1，x2，使得对任意的实数x都有成立，则的最小值为2π.

    其中正确的命题的序号为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的离心率为，且短轴长为2.

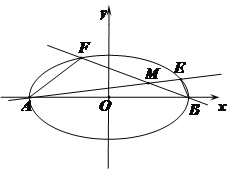
    （1）求椭圆的标准方程；

    （2）已知分别为椭圆的左右顶点， ,，且,直线与分别与椭圆交于两点，

    （i）用表示点的纵坐标；

    （ii）若面积是面积的5倍，求的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】2017年5月27日当今世界围棋排名第一的柯洁在与的人机大战中中盘弃子认输，至此柯洁与的三场比赛全部结束，柯洁三战全负，这次人机大战再次引发全民对围棋的关注，某学校社团为调查学生学习围棋的情况，随机抽取了100名学生进行调查，根据调查结果绘制的学生日均学习围棋时间的频率分布直方图（如图所示），将日均学习围棋时间不低于40分钟的学生称为“围棋迷”.

    （1）请根据已知条件完成下面列联表，并据此资料你是否有95%的把握认为“围棋迷”与性别有关？

    非围棋迷

    围棋迷

    合计

    男

    女

    10

    55

    合计

    （2）为了进一步了解“围棋迷”的围棋水平，从“围棋迷”中按性别分层抽样抽取5名学生组队参加校际交流赛，首轮该校需派两名学生出赛，若从5名学生中随机抽取2人出赛，求2人恰好一男一女的概率.

    查看答案和解析>>

    同步练习册答案