
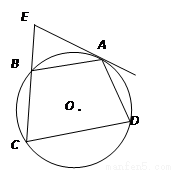
如图,四边形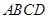 的外接圆为⊙
的外接圆为⊙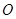 ,
,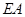 是⊙
是⊙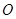 的切线,
的切线,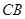 的延长线与
的延长线与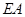 相交于点
相交于点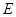 ,
,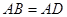 .
.
求证: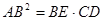 .
.
科目:高中数学 来源: 题型:
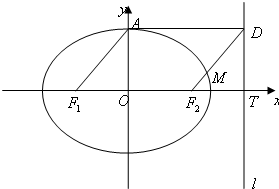 如图,已知椭圆
如图,已知椭圆| x2 |
| a2 |
| y2 |
| b2 |
| TA |
| TM |
查看答案和解析>>
科目:高中数学 来源: 题型:
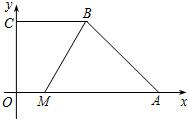 如图,在四边形ABCO中,
如图,在四边形ABCO中,| OA |
| CB |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年云南省毕业生复习第二次统一检测理科数学试卷(解析版) 题型:解答题
如图,四边形 的外接圆为⊙
的外接圆为⊙ ,
, 是⊙
是⊙ 的切线,
的切线, 的延长线与
的延长线与 相交于点
相交于点 ,
, .
.
求证: .
.

查看答案和解析>>
科目:高中数学 来源:2012年全国普通高等学校招生统一考试文科数学(课标卷解析版) 题型:解答题
如图,D,E分别是△ABC边AB,AC的中点,直线DE交△ABC的外接圆与F,G两点,若CF∥AB,证明:

(Ⅰ) CD=BC;
(Ⅱ)△BCD∽△GBD.
【命题意图】本题主要考查线线平行判定、三角形相似的判定等基础知识,是简单题.
【解析】(Ⅰ) ∵D,E分别为AB,AC的中点,∴DE∥BC,
∵CF∥AB, ∴BCFD是平行四边形,
∴CF=BD=AD, 连结AF,∴ADCF是平行四边形,

∴CD=AF,
∵CF∥AB, ∴BC=AF, ∴CD=BC;
(Ⅱ) ∵FG∥BC,∴GB=CF,
由(Ⅰ)可知BD=CF,∴GB=BD,
∵∠DGB=∠EFC=∠DBC, ∴△BCD∽△GBD
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com