
【题目】已知![]() 是抛物线
是抛物线![]() 的焦点,
的焦点,![]() 是抛物线上一点,且
是抛物线上一点,且![]() .
.
(1)求抛物线![]() 的标准方程;
的标准方程;
(2)过点![]() 的动直线
的动直线![]() 交抛物线于
交抛物线于![]() 两点,抛物线上是否存在一个定点
两点,抛物线上是否存在一个定点![]() ,使得以弦
,使得以弦![]() 为直径的圆恒过点
为直径的圆恒过点![]() ?若存在,求出点
?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)存在点
;(2)存在点![]() 符合题意.
符合题意.
【解析】
(1)利用抛物线上的点到焦点的距离与到到准线的距离相等即可求出![]() 的值,即可求出抛物线方程.
的值,即可求出抛物线方程.
(2)假设存在满足条件的点,依题设过点![]() 直线的直线的方程为
直线的直线的方程为![]() ,设
,设![]() ,联立方程由根与系数的关系可得
,联立方程由根与系数的关系可得![]() ;依题可得
;依题可得![]() ,若能得出关于
,若能得出关于![]() 的成立的恒等式,则满足条件的点存在,否则就不存在.
的成立的恒等式,则满足条件的点存在,否则就不存在.
(1)抛物线![]() 的准线方程为
的准线方程为![]() ,
,
所以点![]() 到准线的距离为
到准线的距离为![]() ,又
,又![]() ,
,
由抛物线的定义可得![]() ,所以
,所以![]() ,
,
所以抛物线的方程为:![]() .
.
(2)假设存在点![]() 使以弦
使以弦![]() 为直径的圆恒过点
为直径的圆恒过点![]() ,
,
设过点![]() 直线的直线
直线的直线![]() 的方程为
的方程为![]() ,
,
联立方程![]() 得
得![]() ,
,
设![]() ,则
,则![]() ,
,![]() ;
;
因为点![]() 总是在以弦
总是在以弦![]() 为直径的圆上,
为直径的圆上,
所以![]() ,所以
,所以![]()
由![]() ,
,![]()
所以![]()
即![]()
当![]() 或
或![]() ,等式显然成立;
,等式显然成立;
当![]() 或
或![]() 时,则有
时,则有![]()
即![]() ,则
,则![]() ,
,
即![]()
所以当![]() 时,无论
时,无论![]() 取何值等式都成立,
取何值等式都成立,
将![]() 代入
代入![]() 得
得![]() ,
,
所以存在点![]() 使以弦
使以弦![]() 为直径的圆恒过点
为直径的圆恒过点![]() .
.


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:高中数学 来源: 题型:
【题目】湖北省第二届(荆州)园林博览会于2019年9月28日至11月28日在荆州园博园举办,本届园林博览会以“辉煌荆楚,生态园博”为主题,展示荆州生态之美,文化之韵,吸引更多优秀企业来荆投资,从而促进荆州经济快速发展.在此次博览会期间,某公司带来了一种智能设备供采购商洽谈采购,并决定大量投放荆州市场.已知该种设备年固定研发成本为50万元,每生产一台需另投入80元,设该公司一年内生产该设备![]() 万台且全部售完,每万台的销售收入
万台且全部售完,每万台的销售收入![]() (万元)与年产量
(万元)与年产量![]() (万台)满足如下关系式:
(万台)满足如下关系式: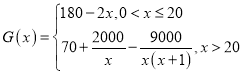 .
.
(1)写出年利润![]() (万元)关于年产量
(万元)关于年产量![]() (万台)的函数解析式;(利润=销售收入-成本)
(万台)的函数解析式;(利润=销售收入-成本)
(2)当年产量为多少万台时,该公司获得的年利润最大?并求最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正方体ABCD-A1B1C1D1中,点M、N分别在AB1、BC1上,且AM=![]() AB1,BN=
AB1,BN=![]() BC1,则下列结论:①AA1⊥MN;②A1C1// MN;③MN//平面A1B1C1D1;④B1D1⊥MN,其中,
BC1,则下列结论:①AA1⊥MN;②A1C1// MN;③MN//平面A1B1C1D1;④B1D1⊥MN,其中,
正确命题的个数是( )

A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,由半圆![]() 和部分抛物线
和部分抛物线![]() 合成的曲线
合成的曲线![]() 称为“羽毛球开线”,曲线
称为“羽毛球开线”,曲线![]() 与
与![]() 轴有
轴有![]() 两个焦点,且经过点
两个焦点,且经过点![]()

(1)求![]() 的值;
的值;
(2)设![]()
![]() 为曲线
为曲线![]() 上的动点,求
上的动点,求![]() 的最小值;
的最小值;
(3)过![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 与“羽毛球形线”相交于点
与“羽毛球形线”相交于点![]() 三点,问是否存在实数
三点,问是否存在实数![]() 使得
使得![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从抛物线![]() 上任意一点P向x轴作垂线段,垂足为Q,点M是线段
上任意一点P向x轴作垂线段,垂足为Q,点M是线段![]() 上的一点,且满足
上的一点,且满足![]()
(1)求点M的轨迹C的方程;
(2)设直线![]() 与轨迹c交于
与轨迹c交于![]() 两点,T为C上异于
两点,T为C上异于![]() 的任意一点,直线
的任意一点,直线![]() ,
,![]() 分别与直线
分别与直线![]() 交于
交于![]() 两点,以
两点,以![]() 为直径的圆是否过x轴上的定点?若过定点,求出符合条件的定点坐标;若不过定点,请说明理由.
为直径的圆是否过x轴上的定点?若过定点,求出符合条件的定点坐标;若不过定点,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系.已知直线l上两点M,N的极坐标分别为(2,0),(![]() ),圆C的参数方程
),圆C的参数方程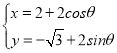 (θ为参数).
(θ为参数).
(Ⅰ)设P为线段MN的中点,求直线OP的平面直角坐标方程;
(Ⅱ)判断直线l与圆C的位置关系.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】A4纸是生活中最常用的纸规格.A系列的纸张规格特色在于:①A0、A1、A2…、A5,所有尺寸的纸张长宽比都相同.②在A系列纸中,前一个序号的纸张以两条长边中点连线为折线对折裁剪分开后,可以得到两张后面序号大小的纸,比如1张A0纸对裁后可以得到2张A1纸,1张A1纸对裁可以得到2张A2纸,依此类推.这是因为A系列纸张的长宽比为![]() :1这一特殊比例,所以具备这种特性.已知A0纸规格为84.1厘米×118.9厘米.118.9÷84.1≈1.41≈
:1这一特殊比例,所以具备这种特性.已知A0纸规格为84.1厘米×118.9厘米.118.9÷84.1≈1.41≈![]() ,那么A4纸的长度为( )
,那么A4纸的长度为( )
A.![]() 厘米B.
厘米B.![]() 厘米C.
厘米C.![]() 厘米D.
厘米D.![]() 厘米
厘米
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某艺术品公司欲生产一款迎新春工艺礼品,该礼品是由玻璃球面和该球的内接圆锥组成,圆锥的侧面用于艺术装饰,如图1.为了便于设计,可将该礼品看成是由圆O及其内接等腰三角形![]() 绕底边
绕底边![]() 上的高所在直线
上的高所在直线![]() 旋转
旋转![]() 而成,如图2.已知圆O的半径为
而成,如图2.已知圆O的半径为![]() ,设
,设![]() ,
,![]() ,圆锥的侧面积为
,圆锥的侧面积为![]() (S圆锥的侧面积
(S圆锥的侧面积![]() (R-底面圆半径,I-母线长))
(R-底面圆半径,I-母线长))
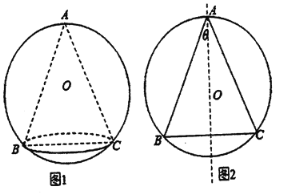
(1)求S关于![]() 的函数关系式;
的函数关系式;
(2)为了达到最佳观赏效果,要求圆锥的侧面积S最大.求S取得最大值时腰![]() 的长度
的长度
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com