练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知三点A(－1,1,2)，B(1,2，－1)，C(a,0,3)，是否存在实数a，使A、B、C共线？若存在，求出a的值；若不存在，说明理由．

    【答案】不存在实数a，使A、B、C共线

    【解析】试题分析: 根据三点共线时线段关系分类列式BC＝AC＋AB或AC＝BC＋AB,利用两点间距离公式代入化简,根据方程解的情况确定是否存在

    试题解析:AB＝＝，

    AC＝＝，

    BC＝

    ＝，

    因为BC>AB，所以，若A，B，C三点共线，有BC＝AC＋AB或AC＝BC＋AB，

    若BC＝AC＋AB，整理得：5a2＋18a＋19＝0，

    此方程无解；

    若AC＝BC＋AB，整理得：5a2＋18a＋19＝0，此方程也无解．

    所以不存在实数a，使A、B、C共线．

    点睛: 两点间距离公式为

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数的定义域是.

    （1）判断在上的单调性，并证明；

    （2）若不等式对任意恒成立，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的离心率，左顶点为.

    （1）求椭圆的方程；

    （2）已知为坐标原点， 是椭圆上的两点，连接的直线平行交轴于点，证明： 成等比数列.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，棱形与正三角形的边长均为2，它们所在平面互相垂直， ，且．

    （1）求证： ；

    （2）若，求二面角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

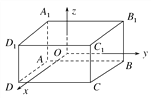
    【题目】如图，已知长方体ABCD－A1B1C1D1的对称中心在坐标原点，交于同一顶点的三个面分别平行于三个坐标平面，顶点A(－2，－3，－1)，求其他七个顶点的坐标．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】【2014全国1理21】设函数，曲线在点处的切线方程为

    （I）求

    （II）证明：

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知圆C:x2+y2-8y+12=0,直线l经过点D(-2,0),且斜率为k.

    (1)求以线段CD为直径的圆E的方程.

    (2)若直线l与圆C相离,求k的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】直线l经过两直线l1:2x-y+4=0与l2:x-y+5=0的交点,且与直线x-2y-6=0垂直.

    (1)求直线l的方程.

    (2)若点P(a,1)到直线l的距离为,求实数a的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设人的某一特征(如眼睛的大小)是由他的一对基因所决定,以d表示显性基因,r表示隐性基因,则具有dd基因的人为纯显性,具有rr基因的人为纯隐性,具有rd基因的人为混合性,纯显性与混合性的人都显露显性基因决定的某一特征,孩子从父母身上各得到一个基因,假定父母都是混合性,问:

    (1)1个孩子显露显性特征的概率是多少?

    (2)“该父母生的2个孩子中至少有1个显露显性特征”,这种说法正确吗?

    查看答案和解析>>

    同步练习册答案