
分析 (1)利用平方关系化弦为切求值;
(2)化切为弦,再由倍角公式及两角和与差的正弦、余弦化简求值.
解答 解:(1)∵$tanθ=-\frac{3}{4}$,
∴1+sinθcosθ-cos2θ=$\frac{{{{sin}^2}θ+{{cos}^2}θ+sinθcosθ-{{cos}^2}θ}}{{{{sin}^2}θ+{{cos}^2}θ}}$
=$\frac{{{{sin}^2}θ+sinθcosθ}}{{{{sin}^2}θ+{{cos}^2}θ}}$=$\frac{{{{tan}^2}θ+tanθ}}{{1+{{tan}^2}θ}}$=$-\frac{3}{25}$;
(2)$\frac{{cos{{40}^0}+sin{{50}^0}(1+\sqrt{3}tan{{10}^0})}}{{sin{{70}^0}\sqrt{1+sin{{50}^0}}}}$
=$\frac{{cos{{40}^0}+sin{{50}°}(1+\frac{{\sqrt{3}sin{{10}^0}}}{{cos{{10}°}}})}}{{cos{{20}°}\sqrt{1+cos{{40}°}}}}$
=$\frac{{cos{{40}^0}+cos{{40}°}\frac{{2sin({{10}^0}+{{30}^0})}}{{cos{{10}°}}}}}{{\sqrt{2}{{cos}^2}{{20}°}}}$
=$\frac{{cos{{40}^0}+\frac{{sin{{80}^0}}}{{cos{{10}^0}}}}}{{\sqrt{2}{{cos}^2}{{20}°}}}$=$\frac{{cos{{40}°}+1}}{{\sqrt{2}{{cos}^2}{{20}°}}}$=$\sqrt{2}$.
点评 本题考查三角函数的化简求值,考查诱导公式、同角三角函数基本关系式及两角和与差的正弦及余弦的应用,是中档题.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案科目:高中数学 来源: 题型:解答题
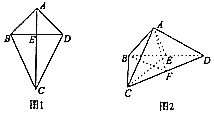 如图1,四边形ABCD中AC⊥BD,CE=2AE=2BE=2DE=2,将四边形ABCD沿着BD折叠,得到图2所示的三棱锥A-BCD,其中AB⊥CD.
如图1,四边形ABCD中AC⊥BD,CE=2AE=2BE=2DE=2,将四边形ABCD沿着BD折叠,得到图2所示的三棱锥A-BCD,其中AB⊥CD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com