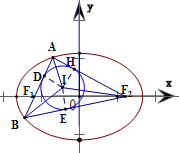
分析:根据椭圆方程求得焦距|F1F2|=6,由椭圆的定义算出△ABF2的周长为4a=20,由圆面积公式算出△ABF2的内切圆半径r=1.利用内切圆的性质把△PF1F2分割成3个三角形,由三角形的面积公式算出△PF1F2的面积等于10,再利用面积相等建立关系式得到关于|y2-y1|的等式,解之即可求得|y2-y1|的值.
解答:解:椭圆
+=1中,a=5,b=4,
∴c=
=3,可得焦点坐标为F
1(-3,0),F
2(3,0).
根据椭圆的定义得|AF
1|+|AF
2|=|BF
1|+|BF
2|=10,
∴△ABF
2的周长为|AB|+|AF
2|+|BF
2|
=(|AF
1|+|AF
2|)+(|BF
1|+|BF
2|)=20
设△ABF
2的内切圆的圆心为I,半径为r,
由内切圆面积S=πr
2=π,解得r=1
∴
S△ABF2=S
△ABI+
S△AF2I+
S△BF2I=
|AB|r+|AF
2|r+|BF
2|r
=
(|AB|+|AF
2|+|BF
2|)×r=
×20×1=10,
又∵
S△ABF2=
|F
1F
2|•|y
2-y
1|,
∴
×6×|y
2-y
1|=10,解得|y
2-y
1|=
.
故选:B
点评:本题给出椭圆的内接三角形的内切圆面积,求|y2-y1|的纵坐标.着重考查了椭圆的标准方程与简单几何性质、三角形的内切圆的性质和三角形的面积公式等知识,属于中档题.解决问题的关键是熟练掌握椭圆的定义与性质,熟练运用三角形的内切圆的有关知识.



