
【题目】如图,在三棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() ,
,![]() 点
点![]() ,
,![]() ,
,![]() 分别为线段
分别为线段![]() ,
,![]() ,
,![]() 的中点,点
的中点,点![]() 是线段
是线段![]() 的中点.求证:
的中点.求证:
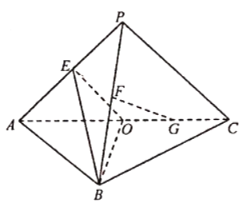
(1)![]() 平面
平面![]() ;
;
(2)![]() .
.
【答案】(1)见解析;(2)见解析
【解析】
(1)连AF交BE于Q,连QO,推导出Q是△PAB的重心,从而FG∥QO,由此能证明FG∥平面EBO.
(2)推导出BO⊥AC,从而BO⊥面PAC,进而BO⊥PA,再求出OE⊥PA,由此能证明PA⊥平面EBO,利用线面垂直的性质可证PA⊥BE.
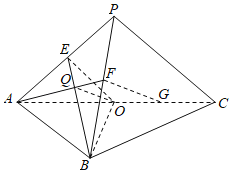
(1)连接AF交BE于Q,连接QO,
因为E,F分别为边PA,PB的中点,
所以Q为△PAB的重心,可得:![]() 2,
2,
又因为O为线段AC的中点,G是线段CO的中点,
所以![]() 2,
2,
于是![]() ,
,
所以FG∥QO,
因为FG平面EBO,QO平面EBO,
所以FG∥平面EBO.
(2)因为O为边AC的中点,AB=BC,
所以BO⊥AC,
因为平面PAC⊥平面ABC,平面PAC∩平面ABC=AC,BO平面ABC,
所以BO⊥平面PAC,
因为PA平面PAC,
所以BO⊥PA,
因为点E,O分别为线段PA,AC的中点,
所以EO∥PC,
因为PA⊥PC,
所以PA⊥EO,
又BO∩OE=O,BO,EO平面EBO,
所以PA⊥平面EBO,
因为BE平面EBO,
所以PA⊥BE.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】设命题![]() 对任意实数
对任意实数![]() ,不等式
,不等式![]() 恒成立;命题
恒成立;命题![]() 方程
方程![]() 表示焦点在
表示焦点在![]() 轴上的双曲线.
轴上的双曲线.
(1)若命题![]() 为真命题,求实数
为真命题,求实数![]() 的取值范围;
的取值范围;
(2)若命题:“![]() ”为真命题,且“
”为真命题,且“![]() ”为假命题,求实数
”为假命题,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 为偶函数,且函数
为偶函数,且函数![]() 图像的两相邻对称轴间的距离为
图像的两相邻对称轴间的距离为![]() .
.
(1)求![]() ,
,![]() 及
及![]() 的值.
的值.
(2)将函数![]() 的图像向右平移
的图像向右平移![]() 个单位,再将得到的图像上每个点的横坐标伸长到原来的
个单位,再将得到的图像上每个点的横坐标伸长到原来的![]() 倍,纵坐标不变,得到函数
倍,纵坐标不变,得到函数![]() 的图像,求
的图像,求![]() 的单调递减区间.
的单调递减区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() 、
、![]() 是两个小区所在地,
是两个小区所在地,![]() 、
、![]() 到一条公路
到一条公路![]() 的垂直距离分别为
的垂直距离分别为![]()
![]() ,
,![]()
![]() ,
,![]() 两端之间的距离为
两端之间的距离为![]()
![]() .
.
(1)某移动公司将在![]() 之间找一点
之间找一点![]() ,在
,在![]() 处建造一个信号塔,使得
处建造一个信号塔,使得![]() 对
对![]() 、
、![]() 的张角与
的张角与![]() 对
对![]() 、
、![]() 的张角相等,试确定点
的张角相等,试确定点![]() 的位置.
的位置.
(2)环保部门将在![]() 之间找一点
之间找一点![]() ,在
,在![]() 处建造一个垃圾处理厂,使得
处建造一个垃圾处理厂,使得![]() 对
对![]() 、
、![]() 所张角最大,试确定点
所张角最大,试确定点![]() 的位置.
的位置.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商店经营的消费品进价每件14元,月销售量![]() (百件)与销售价格p(元)的关系如下图,每月各种开支2000元.
(百件)与销售价格p(元)的关系如下图,每月各种开支2000元.

(1)写出月销售量![]() (百件)与销售价格p(元)的函数关系;
(百件)与销售价格p(元)的函数关系;
(2)写出月利润y(元)与销售价格p(元)的函数关系:
(3)当商品价格每件为多少元时,月利润最大?并求出最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,侧面
中,侧面![]() 底面ABCD,侧棱
底面ABCD,侧棱![]() ,底面ABCD为直角梯形,其中
,底面ABCD为直角梯形,其中![]() ,
,![]() ,
,![]() ,O为AD中点.
,O为AD中点.

(1)求异面直线PB与CD所成角的余弦值;
(2)线段AD上是否存在点Q,使得它到平面PCD的距离为![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com