
 (本小题满分18分)如图,将圆分成
(本小题满分18分)如图,将圆分成![]() 个扇形区域,用3种不同颜色给每一个扇形区域染色,要求相邻区域颜色互异,把不同的染色方法种数记为
个扇形区域,用3种不同颜色给每一个扇形区域染色,要求相邻区域颜色互异,把不同的染色方法种数记为![]() 。求
。求
(Ⅰ)![]() ;
;
(Ⅱ)![]() 与
与![]() 的关系式;
的关系式;
(Ⅲ)数列![]() 的通项公式
的通项公式![]() ,并证明
,并证明![]() 。
。
解析:(Ⅰ) 当![]() 时,不同的染色方法种数
时,不同的染色方法种数![]() ,……………………1分
,……………………1分
当![]() 时,不同的染色方法种数
时,不同的染色方法种数![]() ,……………………………2分
,……………………………2分
当![]() 时,不同的染色方法种数
时,不同的染色方法种数![]() ,……………………………3分
,……………………………3分
当![]() 时,分扇形区域1,3同色与异色两种情形
时,分扇形区域1,3同色与异色两种情形
∴不同的染色方法种数![]() 。…………………4分
。…………………4分
(Ⅱ)依次对扇形区域![]() 染色,不同的染色方法种数为
染色,不同的染色方法种数为![]() ,其中扇形区域1与
,其中扇形区域1与![]() 不同色的有
不同色的有![]() 种,扇形区域1与
种,扇形区域1与![]() 同色的有
同色的有![]() 种
种
∴![]() …………………………………………………8分
…………………………………………………8分
(Ⅲ)∵![]()
∴![]()
![]()
………………
![]()
将上述![]() 个等式两边分别乘以
个等式两边分别乘以![]() ,再相加,得
,再相加,得
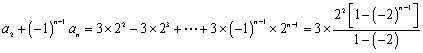 ,
,
∴![]() ,…………………………………………………13分
,…………………………………………………13分
从而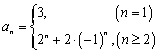 。………………………………………14分
。………………………………………14分
(Ⅲ)证明:当![]() 时,
时,![]()
当![]() 时,
时,![]() ,
,
当![]() 时,
时,
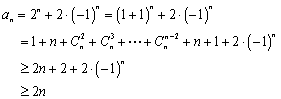 ,
,


科目:高中数学 来源: 题型:
(本小题满分18分)已知数列{an}、{bn}、{cn}的通项公式满足bn=an+1-an,cn=bn+1-bn(n∈N*?),若数列{bn}是一个非零常数列,则称数列{an}是一阶等差数列;若数列{cn}是一个非零常数列,则称数列{an}是二阶等差数列?(1)试写出满足条件a1=1,b1=1,cn=1(n∈N*?)的二阶等差数列{an}的前五项;(2)求满足条件(1)的二阶等差数列{an}的通项公式an;(3)若数列{an}首项a1=2,且满足cn-bn+1+3an=-2n+1(n∈N*?),求数列{an}的通项公式
查看答案和解析>>
科目:高中数学 来源:2011-2012学年上海市长宁区高三教学质量测试理科数学 题型:解答题
(本小题满分18分) 本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
(文)已知数列 中,
中,
(1)求证数列 不是等比数列,并求该数列的通项公式;
不是等比数列,并求该数列的通项公式;
(2)求数列 的前
的前 项和
项和 ;
;
(3)设数列 的前
的前 项和为
项和为 ,若
,若 对任意
对任意 恒成立,求
恒成立,求 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年上海市长宁区高三教学质量测试理科数学 题型:解答题
本小题满分18分) 本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
设函数 是定义域为R的奇函数.
是定义域为R的奇函数.
(1)求k值;
(2)(文)当 时,试判断函数单调性并求不等式f(x2+2x)+f(x-4)>0的解集;
时,试判断函数单调性并求不等式f(x2+2x)+f(x-4)>0的解集;
(理)若f(1)<0,试判断函数单调性并求使不等式 恒成立的
恒成立的 的取值范围;
的取值范围;
(3)若f(1)=,且g(x)=a 2x+a - 2x-2m f(x) 在[1,+∞)上的最小值为-2,求m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com